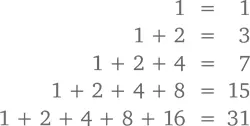Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Сектор с квадратиком имеет размер 2 k на 2 k , что значит, что его можно полностью выложить тримино (исходя из того, что наше утверждение истинно при n = k ). Затем положим одну костяшку тримино в центр доски так, чтобы она находилась одновременно в трех оставшихся секторах, каждый из которых также равен 2 k на 2 k и в каждом из которых у нас теперь есть по одному квадратику, что делает их абсолютно похожими на первый. Ну а если можно полностью выложить неперекрывающимися тримино каждую часть (размером 2 k на 2 k ) доски, то ими можно выложить и всю доску размером 2 k +1на 2 k +1.☺

Последнее тождество имеет много полезных применений. Давайте докажем его по индукции, добавив парочку других способов. Какова сумма первых n чисел, которые получаются при возведении 2 в последовательные степени, начиная с 2 0= 1?

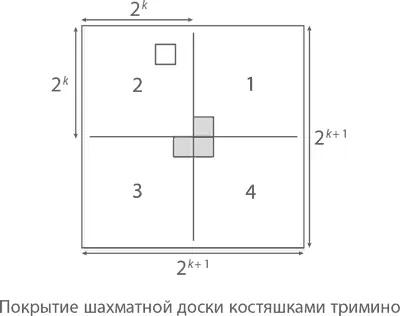
Приступим к сложению:

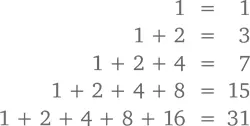
Видите закономерность? Каждая сумма на 1 меньше следующего числа, получаемого от возведения 2 в степень. Все это сводится вот к чему.

Теорема:Для n ≥ 1

Доказательство по индукции:Как мы уже отмечали, утверждение является верным при n = 1 (а также 2, 3, 4 и 5). При n = k мы можем утверждать, что

Добавив к обеим частям следующее число, получаемое при возведении 2 в степень (то есть 2 k ), приходим к

В 4 и 5 главах мы подтвердили множество закономерностей, находя ответ двумя разными способами. Возможно, комбинаторный подход покажется вам наиболее ценным.

Вопрос: В хоккейной команде n игроков (соответственно, их свитера пронумерованы от 1 до n ). Созывается пресс-конференция, на которую должен прийти хотя бы один игрок. Чему равно количество возможных «составов» команды на этой пресс-конференции?

Ответ 1: У каждого игрока два варианта: идти или не идти. Значит, у команды в целом есть 2 n вариантов. Но из этого числа нам нужно вычесть единицу, чтобы исключить вероятность того, что на конференцию не придет никто. В итоге получается 2 n – 1.

Ответ 2: За основу «состава» положим хоккеиста с наибольшим номером на свитере. «Состав» с единицей в качестве наибольшего числа всего 1, с двойкой их 2 (потому что хоккеист № 2 может пойти либо в одиночестве, либо в компании хоккеиста № 1), с тройкой – 4 (потому что хоккеист № 3 может пойти либо один, либо в компании хоккеиста № 2, который точно так же может позвать, а может и не позвать с собой хоккеиста № 1). Следуя этой логике и дальше, мы увидим, что всего возможных «составов» будет 2 n –1, ведь хоккеист № n будет обязан пойти на конференцию, а у каждого из его товарищей (начиная с № 1 и заканчивая № n – 1), которых он может позвать с собой, будет по 2 варианта выбора. То есть 1 + 2 + 4 +… + 2 n–1 .

Оба результата верны, а значит, равны. Таким образом, получается, что 1 + 2 + 4 +… + 2 n–1 = 2 n – 1.☺

При всех достоинствах комбинаторного метода наиболее простым здесь будет алгебраический – схожий с тем, который мы использовали для преобразования периодической десятичной дроби в простую.

Алгебраическое доказательство:

Удвоив обе части, получим

Вычтем первое уравнение из второго, что позволит нам избавиться от всего лишнего и оставить только S из первого и 2 S из второго, то есть

Теорема эта – ключ к двоичной системе, имеющей огромное практическое значение: именно на ее основе проводят числовые операции все компьютеры. Смысл ее заключается в том, чтобы представить любое число как уникальную сумму различных степеней основания числа 2. Например,