Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Если учесть исторические отношения музыки с числами, на ум сам собой приходит вопрос, играло ли золотое сечение (или числа Фибоначчи) ту или иную роль как в развитии музыкальных инструментов, так и в музыкальных композициях.

Золотое сечение очень часто применяется в конструкции скрипки. Как правило, очертания корпуса скрипки составляют не менее двенадцати кривых – они и создают ее характерные изгибы. Центром самой плоской кривой, внизу, как правило, служит точка, делящая центральную линию скрипки в золотом сечении.

Пожалуй, самые знаменитые скрипки – это инструменты работы Антонио Страдивари (1644–1737) из итальянского города Кремона. На чертежах мастера (рис. 85) видно, что Страдивари особенно тщательно рассчитывал геометрическое положение так называемых эфов – прорезей на передней части корпуса, – и помещал их в точки, определенные золотым сечением. Однако лишь немногие – возможно, таких и вовсе нет, – полагают, будто скрипки Страдивари обязаны своим непревзойденным качеством и звучанием именно золотому сечению. Гораздо чаще «секретом» Страдивари называют лак, клей, древесину и, конечно, мастерство изготовителя. Многие специалисты сходятся на том, что популярность скрипок XVIII века в целом объясняется их прекрасным звучанием в больших концертных залах. Большинство этих специалистов скажет вам также, что никакого «секрета» у скрипок Страдивари нет: это прекрасно выполненное изделие, которое вполне можно повторить, сумма тщательно изготовленных частей, составляющих добротное целое.

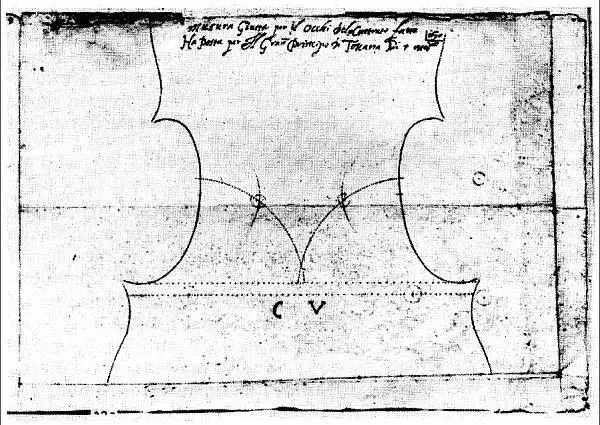
Рис. 85

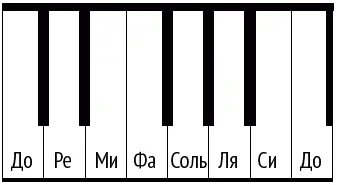
Рис. 86

В связи с числами Фибоначчи упоминают и другой музыкальный инструмент – фортепиано. Октава на клавиатуре фортепиано состоит из тринадцати клавиш, восьми белых и пяти черных (рис. 86). Черные клавиши, в свою очередь, объединены в две группы – две и три. Так вышло, что числа 2, 3, 5, 8 и 13 – последовательные числа Фибоначчи. А то, что главная тональность – до мажор, объясняется отчасти тем, что эту гамму играют только на белых клавишах. Однако очень может быть, что связь между клавиатурой фортепиано и числами Фибоначчи – всего лишь случайность, порождающая необоснованные домыслы. Во-первых, обратим внимание, что хроматическая гамма – на рисунке от ноты «до» до ноты «си» – на которой строится вся западная музыка, состоит на самом деле из двенадцати, а не тринадцати полутонов. Одна и та же нота «до» играется в октаве дважды, дабы подчеркнуть завершенность цикла. Во-вторых и в-главных, расположение клавиш в два ряда, когда диезы и бемоли сгруппированы по два и по три в верхнем ряду, восходит к началу XV века, то есть сложилась задолго до публикации книги Пачоли и тем более до любых серьезных исследований чисел Фибоначчи.

Страстные поклонники золотого сечения утверждают, что это соотношение обладает особыми эстетическими свойствами не только в изобразительном искусстве, но и в музыке, где оно создает особенно приятные созвучия. Например, в книгах о золотом сечении сплошь и рядом пишут, что многие считают, будто самые благозвучные музыкальные интервалы – это большая и малая сексты и что эти интервалы связаны с золотым сечением. Для чистого музыкального тона характерна определенная частота, выраженная в количестве колебаний в секунду, и определенная амплитуда, определяющая громкость в конкретный момент времени. Обычно для настраивания музыкальных инструментов используют ноту ля, которой соответствует частота 440 колебаний в секунду. Большая секста получается из сочетания ля с до: последней соответствует частота около 264 колебаний в секунду. Отношение частот 440/264 сокращается до 5/3 – то есть до отношения двух последовательных чисел Фибоначчи. Большая секста получается, если взять верхнее до (528 колебаний в секунду) и ми (330 колебаний в секунду). В этом случае отношение 528/330 сокращается до 8/5, то есть тоже до отношения двух последовательных чисел Фибоначчи – это уже очень близко к золотому сечению (напомню, что отношения последовательных чисел Фибоначчи стремятся к золотому сечению). Однако и здесь, как и в живописи, понятие «самого благозвучного» музыкального интервала несколько неоднозначно.

Инструменты, ноты у которых фиксированы, например, фортепиано, настраивают по «равномерно темперированному строю», который популяризировал Бах, где каждый полутон обладает таким же отношением частот, что и следующий, поэтому легко играть в любой тональности. Отношение двух соседних частот у хорошо темперированного инструмента равно 2 1/12(то есть корень 12 степени из 2). Откуда взялось это число? Его происхождение восходит к Древней Греции. Вспомним, что октава получается, если поделить струну на две равные части (то есть соотношение частот должно быть 2 к 1), а квинта – если соотношение частот будет 3 к 2 (то есть при делении струны на две части – две трети и одна треть). Один из вопросов, особенно занимавших пифагорейцев, состоял в том, можно ли создать целое число октав, повторяя процедуру создания квинты (то есть последовательно применяя соотношение частот 3 к 2). В математических терминах это все равно что спросить, существуют ли два целых числа n и m, такие, что (3/2) n = 2 m . Как выясняется, целых чисел, удовлетворяющих этому равенству, нет, однако при n = 12 и m = 7 мы подходим к решению довольно близко, ведь по странному совпадению 2 1/12примерно равняется 3 1/19(корень 19 степени из 3). Поэтому двенадцать частот октавы – это приблизительно равные степени базового соотношения частот 2 1/12. Кстати, хотите верьте, хотите нет, но 19/12 = 1,58, не так уж далеко от φ.