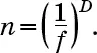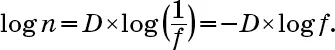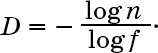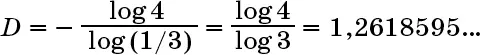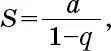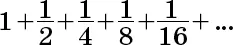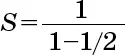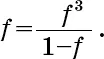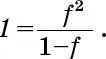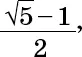Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Отношение между количеством субобъектов n, коэффициентом сокращения длины f и числом измерений D равно

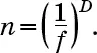
Если положительное число А записывается в виде А = 10 L , то L мы называем логарифмом (по основанию 10) числа А и записываем это так: L = log A. Иначе говоря, равенства А = 10 L и L = log A тождественны. Правила логарифмов таковы:

1. Логарифм произведения есть сумма логарифмов:

log (A × B ) = log A + log B.

2. Логарифм отношения есть разность логарифмов

log ( A / B ) =log A – log B.

3. Логарифм степени числа – это степень, умноженная на логарифм числа:

log A m = m × log A.

Поскольку 10 0 = 1, по определению логарифма log 1 = 0. Поскольку 10 1 = 10, 10 2 = 100 и так далее, получаем, что log 10 = 1, log 100 = 2 и т. д. Следовательно, логарифм любого числа от 1 до 10 – это число от 0 до 1, логарифм любого числа от 10 до 100 – это число от 1 до 2 и т. д.

Если мы возьмем логарифм (по основанию 10) обеих частей вышеприведенного равенства (описывающего отношения между n, f и D), то получим

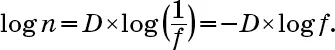
Если теперь поделить обе части на log f , мы получим

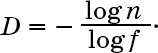
Скажем, в случае снежинки Коха каждая кривая содержит четыре «подкривые» в одну треть длины, поэтому n = 4, f = 1/3, и получаем

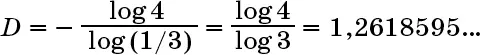
Рассмотрим рис. 116, а , и увидим, что условие соприкосновения двух веток состоит в простом требовании, чтобы сумма всех горизонтальных длин постоянно уменьшающихся веток с длинами начиная от f 3была равна горизонтальной составляющей большой ветки длиной f. Все горизонтальные составляющие – это общая длина, умноженная на косинус угла, величиной 30 градусов. Поэтому получаем

f × cos 30° = f 3× cos 30° + f 4× cos 30° + f 5× cos 30° + …

Поделим это выражение на cos 30° – и получим

f = f 3 + f 4 + f 5 + f 6 + …

Сумма правой части – это сумма бесконечной геометрической прогрессии, то есть каждый ее член равен предыдущему, умноженному на константу, в которой первый член – это f 3, а отношение двух последовательных членов равно f. В целом сумма S бесконечной геометрической прогрессии с первым членом а и отношением последовательных членов q равна

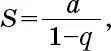
Например, сумма прогрессии

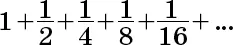
где a = 1 и q = 1/2, равна

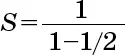
В нашем случае из вышеприведенного уравнения следует

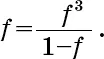
Делим обе части на f и получаем

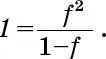
Умножаем на (1– f) , сокращаем и получаем квадратное уравнение

f 2 + f – 1 = 0,

положительный корень которого равен

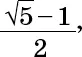
То есть 1/φ.

Согласно закону Бенфорда, вероятность P, что цифра D появится на первом месте, составляет (логарифм по основанию 10)

P = log (1 + 1/D).

Следовательно, для D = 1

P = log (1 + 1) = log 2 = 0,30.

Для D = 2

P = log (1 + 1/2) = log 1,5 = 0,176,

И так далее. Для D = 9,

P = log (1 + 1/9) = log (10/9) = 0,046.

Согласно обобщенной формулировке закона вероятность того, что первые три цифры будут, к примеру, 1, 5 и 8, равна

P = log (1 + 1/158) = 0,0027.

Доказательство Евклида, что существует бесконечное множество простых чисел, основано на методе reductio ad absurdum . Сначала Евклид предполагает, что верно противоположное: простых чисел существует лишь ограниченное множество. Однако, если это правда, одно из них должно быть самым большим простым числом. Обозначим самое большое простое число как P. Затем Евклид выводит новое простое число по следующему алгоритму: он перемножает все простые числа, начиная с 2 и до (включая) Р , и прибавляет к произведению единицу. Получается новое число