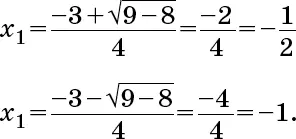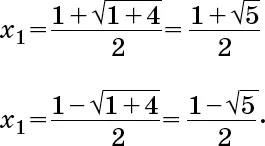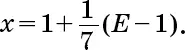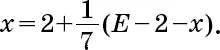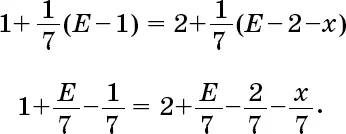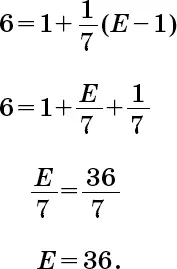Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Площадь треугольника равна половине произведения его основания на высоту, проведенную к основанию. У треугольника TBC основание BC равно 2а , а высота ТА равна с . Следовательно, площадь треугольника равна с × а . Мы хотим показать, что если квадрат высоты пирамиды h 2равен площади ее треугольной стороны s × a, то s/a равно золотому сечению.

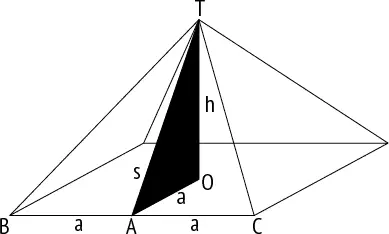
Дано, что

h 2 = s × a.

Применив теорему Пифагора к прямоугольному треугольнику TOA, получаем

s 2 = h 2 + a 2.

Теперь подставим значение h 2из первого равенства и получим

s 2 = s × a + a 2.

Разделим обе части на a 2и получим

(s/a) 2 = (s/a) + 1.

Иными словами, если мы обозначим s/a как x, у нас получится квадратное уравнение

x 2 = x + 1.

В главе 4 показано, что именно это уравнение и описывает золотое сечение.

Одна из теорем в «Началах» доказывает, что если у двух треугольников одинаковые углы, эти треугольники подобны . А это значит, что форма у этих треугольников совершенно одинаковая и длины сторон соответственно пропорциональны. Если одна сторона одного треугольника вдвое длиннее соответствующей стороны второго треугольника, то это справедливо и по отношению к остальным сторонам.

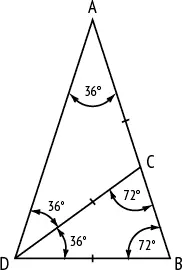
Треугольники ADB и DBC подобны, поскольку у них одинаковые углы. Следовательно, отношение AB/DB, то есть отношение сторон треугольников ADB и DBC, равно DB/BC, то есть отношению оснований этих треугольников.

AB/DB = DB/BC.

Однако эти треугольники также равнобедренные, поэтому

DB = DC = AC.

Из вышеприведенных равенств следует, что

AC/BC = AB/AC,

Что означает (согласно определению Евклида), что точка C делит отрезок AB в золотом сечении. Поскольку AD = AB и DB = AC, получаем также, что AD/DB = φ.

Квадратные уравнения – это уравнения, имеющие вид

ax 2 + bx + c = 0,

где a, b, c – произвольные числа. Например, в уравнении 2 x 2+ 3 x + 1 = 0 имеем a = 2, b = 3, c = 1.

Общая формула для поиска двух корней уравнения:

В вышеприведенном примере

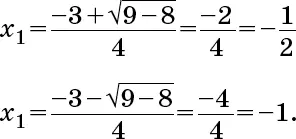
В уравнении, описывающем золотое сечение,

x 2 – x – 1 = 0,

a = 1, b = –1, c = –1, следовательно, корни:

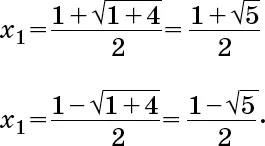
Задачу о дележе наследства можно решить следующим образом. Обозначим все наследство как E, а долю каждого из сыновей в безантах – как x (по условию, все они делят наследство поровну).

Первый сын получил

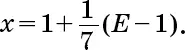
Второй сын получил

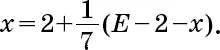
Приравниваем их доли:

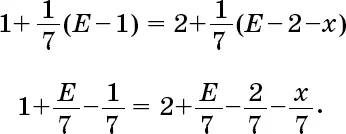
Упрощаем:

x/7 = 6/7

x = 6.

Следовательно, каждому из сыновей досталось по 6 безантов.

Подставив эту величину в первое равенство, получаем:

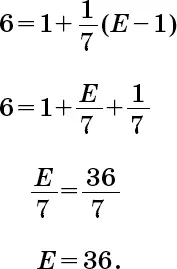
Сумма наследства составила 36 безантов. Следовательно, количество сыновей 36/6 = 6.

А вот как выглядит решение Фибоначчи.

Сумма наследства должна представлять собой такое число, чтобы если прибавить к нему 1 раз по 6, одно делилось бы на 1 плюс 6, то есть на 7, а если прибавить к нему 2 раза по 6, оно делилось бы на 2 плюс 6, то есть на 8, если же прибавить к нему 3 раза по 6, оно делилось бы на 3 плюс 6, то есть на 9, и т. д. Такое число – 36. 1/7 от (36 – 1/7) – это 35/7, плюс 1 – это 42/7, или 6, и это и есть сумма, которую получил каждый из сыновей; общая сумма наследства, поделенная на долю каждого из сыновей, дает нам число сыновей, то есть 36/6 равно 6.