Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Если принять общие определения эволюции, допускающей квантовые скачки, и естественного отбора, действующего в течение длительного времени, то, пожалуй, можно найти объяснение «непостижимой» эффективности математики. Наша математика – символическая репрезентация вселенной в том виде, в каком мы ее воспринимаем , и могущество математики постоянно растет благодаря изысканиям человека.

Джеф Раскин, создатель компьютера «Макинтош» в корпорации «Эппл», подчеркивает иной аспект – эволюцию человеческой логики. В эссе об эффективности математики, опубликованном в 1998 году, Раскин приходит к выводу, что «человеческая логика [курсив мой. – М. Л. ] навязана нам физическим миром и поэтому соответствует ему. Математика выведена из логики. Вот почему математика точно описывает физический мир».

В пьесе «Тамерлан великий», где идет речь о герое-злодее маккиавеллиевского толка, который одновременно может быть и нежной душой, и жестоким убийцей, великий английский драматург Кристофер Марло (1564–1593) признает страсть человека к познанию Вселенной:

Золотое сечение есть продукт геометрии, которую изобрели люди. Однако люди не представляли себе, в какую волшебную страну заведет их это изобретение. Если бы мы не изобрели геометрию, то, вероятно, вообще не знали бы ничего о золотом сечении. Однако – кто знает? – возможно, мы получили бы его в результате работы короткой компьютерной программы.

Мы хотим доказать, что для любых целых чисел p и q, таких, что p > q, три числа: p 2 – q 2; 2 pq; p 2 + q 2формируют пифагорову тройку. Иначе говоря, нам надо доказать, что сумма квадратов первых двух чисел равна квадрату третьего.

Для этого мы обратимся к общим формулам сокращенного умножения, справедливым для любых a и b:

(a + b) 2 = (a + b) × (a + b) = a 2+ ab + ba + b 2 = a 2+ 2 ab + b 2

(a – b) 2 = (a – b) × (a – b) = a 2 – ab – ba + b 2 = a 2 – 2 ab – b 2.

На основании этих формул квадрат первого числа равен

(p 2 – q 2 ) 2 = p 4 – 2 p 2 q 2+ q 4.

Сумма первых двух квадратов равна

p 4 – 2 p 2 q 2+ q 4+ 4 p 2 q 2 = p 4+ 2 p 2 q 2+ q 4.

Квадрат третьего числа равен

(p 2+ q 2 ) 2 = p 4+ 2 p 2 q 2+ q 4.

Итак, мы видим, что квадрат третьего числа равен сумме квадратов первых двух чисел независимо от значений p и q.

Мы хотим доказать, что диагональ и сторона правильного пятиугольника несоизмеримы, то есть у них нет общей меры.

Общий принцип доказательства по методу reductio ad absurdum приведен в конце главы 2.

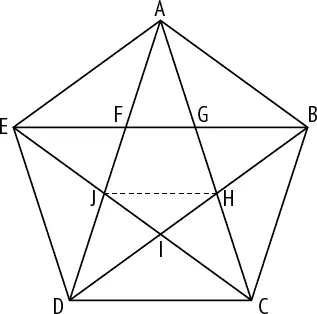
Обозначим сторону правильного пятиугольника ABCDE как s 1, а диагональ – как d 1. Из свойств равнобедренных треугольников легко вывести, что AB = AH и HC = HJ. Теперь обозначим сторону меньшего правильного пятиугольника FGHIJ как s 2и его диагональ как d 2. Очевидно, что

AC = AH + HC = AB + HJ.

Следовательно,

d 1 = s 1+ d 2или d 1 – s 1 = d 2.

Если у d 1и s 1есть какая-либо общая мера, значит, и d 1, и s 1представляют собой целое произведение этой общей меры. Следовательно, существует также общая мера d 1 – s 1, то есть d 2. Подобным же образом равенства

AG = HC = HJ

AH = AB

и

AH = AG + GH

AB = HJ + GH

дают нам

s 1 = d 2 + s 2

или

s 1 – d 2 = s 2.

Поскольку на основании нашего предположения общая мера для s 1и d 1представляет собой также общую меру для d 2, последнее равенство доказывает, что она же еще и общая мера для s 2. Поэтому мы обнаруживаем, что та единица, которая измеряет s 1и d 1, измеряет также s 2 and d 2. Продолжать этот процесс можно до бесконечности, рассматривая правильные пятиугольники все меньшего и меньшего размера. Тогда мы получим, что та же единица, которая служит общей мерой стороны и диагонали первого правильного пятиугольника, служит общей мерой и для всех других пятиугольников, сколь бы крошечными они ни становились. Поскольку очевидно, что так быть не может, следовательно, наше первоначальное предположение, что у стороны и диагонали правильного пятиугольника есть общая мера, ложно, что и доказывает, что s 1и d 1несоизмеримы.