Калеб Шарф - Ошибка Коперника. Загадка жизни во Вселенной

Первый вопрос, с которого начинался список, славился издавна. Называлась задача просто – «Гравитационная задача n тел» [116] Эта знаменитая задача математической физики упоминается в исследовательской литературе сплошь и рядом. Существует множество точных (и очень затейливых) решений для сугубо частных случаев, см., например, Cristopher Moore. Braids in Classical Dynamics // Physical Review Letters 70 (1993): 3675–79, а также чудесные анимационные ролики на сайте http://tuvalu.santafe.edu/~moore/gallery.html. . У этой задачи богатая история: она была сформулирована еще в конце XVII века, когда Исаак Ньютон опубликовал законы движения и тяготения. Законы Ньютона прекрасно объясняли форму планетных орбит, и на первый взгляд казалось, будто с их помощью можно рассчитать движение любого набора тел, вовлеченных в гравитационное взаимодействие – и трех тел, и четырех, и произвольного числа n. Ведь все тела притягивают друг друга с силой, которую легко вывести из закона всемирного тяготения Ньютона. Знаешь начальные условия – следовательно, имеешь возможность выполнить все подсчеты с какой угодно точностью.

Рассчитать движение двух тел, например, Солнца и какой-нибудь одной планеты, было относительно просто, однако Ньютон быстро понял, что если имеешь дело с более сложной системой, получается совсем другая история. Как видно, великого Исаака очень сердило, что он не может найти способ решить уравнения, и он писал: «Если не ошибаюсь, рассмотреть все случаи движения одновременно и определить их по точным законам и при помощи простых вычислений – задача, которая превосходит возможности человеческого разума».

Ньютон был, как, впрочем, и всегда, совершенно прав. Да, ни несколько строчек алгебраических выкладок, ни даже интегральное исчисление не дают математической кривой, которая описывала бы гравитационное взаимодействие n тел. Как и утверждал великий ученый, задача n тел оставалась нерешенной – к вящей досаде физиков и математиков. Нужно было качественное математическое доказательство его слов – а может быть (все может быть), просто несколько более хитроумный подход к решению.

По правде говоря, за время, прошедшее между Ньютоном и Пуанкаре, был достигнут заметный прогресс и найдены довольно точные способы приближенного расчета орбитального движения планет. К концу XVIII века ученые Пьер-Симон Лаплас и Жозеф-Луи Лагранж разработали по набору математических инструментов, способных как минимум предсказать общую картину движения в системе из множества планет за тысячи, а может быть, и миллионы лет. Отчасти секрет был в сугубо технических методах решения. И Лаплас, и Лагранж понимали, что орбиты в системе из множества тел «квазипериодичны»: влияние одних планет на другие означает, что каждая из них будет описывать полные круги по орбите за не совсем одинаковые промежутки времени. И при помощи определенных математических трюков можно опереться на это качество и предсказать общие тенденции в орбитальном движении в системе.

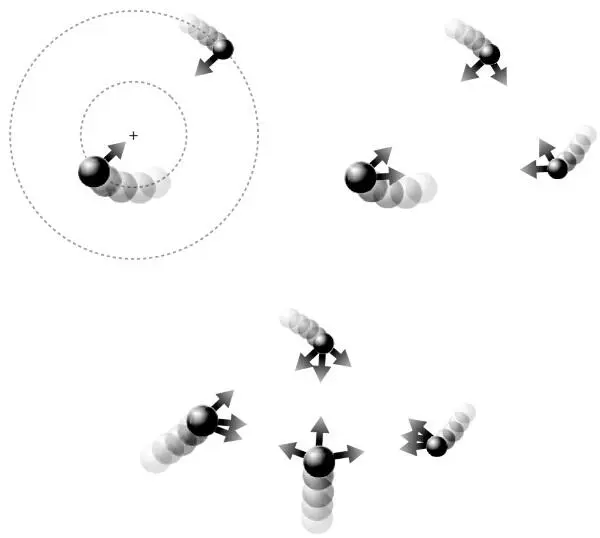
Рис. 9. Наглядная иллюстрация того, как стремительно возрастает сложность системы из тел, вовлеченных в гравитационное взаимодействие. Вверху слева изображены два тела, которые притягивают друг друга и вращаются по орбитам. Ситуация стабильна и поддается расчетам. Однако если тел уже три (вверху справа), требуются 3 набора координат в трехмерном пространстве, 3 трехмерных вектора скорости и 6 трехмерных векторов силы. Четыре тела (внизу) – 4 набора координат, четыре вектора скорости и 12 векторов силы, и все трехмерное, и все действует одновременно. Неудивительно, что Ньютон оставил попытки искать алгебраическое решение этой задачи.

Главный недостаток этих методов состоял в том, что они не позволяли отслеживать каждый момент в движении системы, а, в сущности, вычисляли средние значения сил, с которыми планеты притягивают друг друга и нарушают орбиты друг друга от оборота к обороту. Это очень хитроумные методы, ими и сегодня пользуются, чтобы получить ответы на вопросы о поведении планетных систем в целом, особенно для краткосрочных прогнозов. В свое время эти методы считались также доказательством детерминистической природы гравитационных систем, которые виделись частью «заводной Вселенной», приводимой в движение законами Ньютона.

Однако, несмотря на внешний лоск, это всего-навсего приближенные вычисления, гениальные математические фокусы, которые дают ответы на некоторые вопросы, но не на все. И к концу XIX века становилось все яснее, что нельзя ни пренебрегать всеми силами, которые участвуют в формировании траектории планеты в будущем, ни упрощать их.