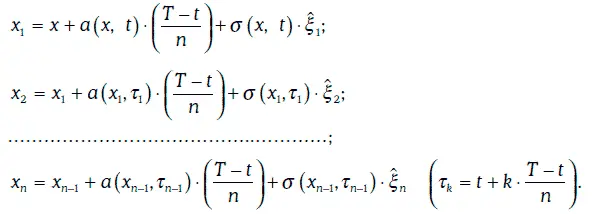Алексей Лобанов - Энциклопедия финансового риск-менеджмента
Здесь есть возможность читать онлайн «Алексей Лобанов - Энциклопедия финансового риск-менеджмента» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Город: Москва, Год выпуска: 2019, ISBN: 2019, Жанр: management, management, popular_business, на русском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Энциклопедия финансового риск-менеджмента
- Автор:
- Жанр:
- Год:2019
- Город:Москва
- ISBN:978-5-9614-2284-9
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Энциклопедия финансового риск-менеджмента: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Энциклопедия финансового риск-менеджмента»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Книга предназначена для профессионалов, непосредственно занимающихся оценкой и управлением рисками, преподавателей, студентов и аспирантов экономических факультетов вузов. Она также может использоваться для подготовки к сдаче международных экзаменов по финансовому риск-менеджменту на получение сертификатов Financial Risk Manager (FRM®) и Professional Risk Manager (PRM®).



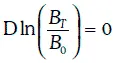 и зависимость
и зависимость 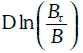 от времени должна иметь вид, изображенный на рис. 1.31.
от времени должна иметь вид, изображенный на рис. 1.31.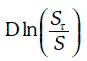 растет во времени линейно.
растет во времени линейно.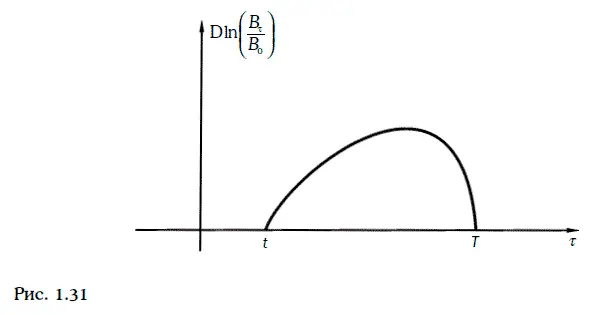
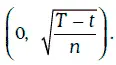 Тогда для последовательности случайных чисел δ 1, δ 2…., δ nбудет построена соответствующая последовательность значений
Тогда для последовательности случайных чисел δ 1, δ 2…., δ nбудет построена соответствующая последовательность значений 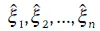 случайной величины ξ, а траектория случайного процесса Ито будет определяться точками:
случайной величины ξ, а траектория случайного процесса Ито будет определяться точками: