2. 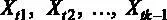 ,
, 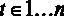 – детерминированные величины.
– детерминированные величины.
3. 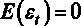 – математическое ожидание ошибок равно нулю,
– математическое ожидание ошибок равно нулю, 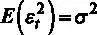 , дисперсия ошибок не зависит от номера наблюдения.
, дисперсия ошибок не зависит от номера наблюдения.
4. 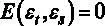 ,
, 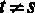 – совместное математическое ожидание ошибок разных наблюдений равно нулю.
– совместное математическое ожидание ошибок разных наблюдений равно нулю.
5. Если выполняется дополнительная предпосылка о нормальном распределении ошибок 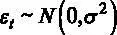 , то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
, то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
Подробнее о предпосылках линейной регрессионной модели можно прочесть в [2, 3].
2. Оценка линейной регрессионной модели
Рассмотрим множественную линейную регрессию
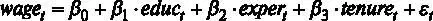 ,
, 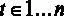 ,
,
где 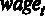 – средний уровень заработной платы в час в долларах,
– средний уровень заработной платы в час в долларах, 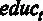 – образование в годах,
– образование в годах, 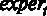 – общий стаж работы в годах,
– общий стаж работы в годах, 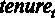 – опыт работы у текущего работодателя, в годах,
– опыт работы у текущего работодателя, в годах, 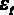 – ошибка регрессии, n – число наблюдений [ файл с данными wage1.gdt ].
– ошибка регрессии, n – число наблюдений [ файл с данными wage1.gdt ].
Для того чтобы оценить предложенную модель по методу наименьших квадратов (МНК), используем команду меню Модель – Метод наименьших квадратов .
В появившемся диалоговом окне в поле Зависимая переменная помещаем переменную 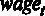 (для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная . Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).
(для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная . Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).
Для дальнейшего удобства можно поставить галочку в окошке Установить по умолчанию . Это делается для того, чтобы при изменении спецификации исследуемой модели зависимая переменная не менялась. В окно Регрессоры отправляем регрессоры модели – это переменные 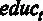 ,
, 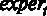 ,
, 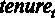 .
.
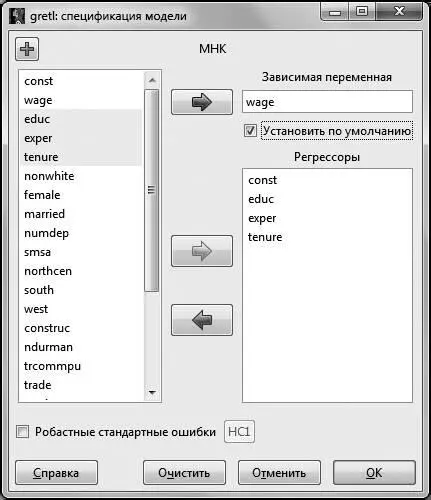
Рис. 2.1
После этого нажимаем ОК . В результате коэффициенты модели были оценены методом наименьших квадратов. Результат оценки представлен на рис. 2.2.
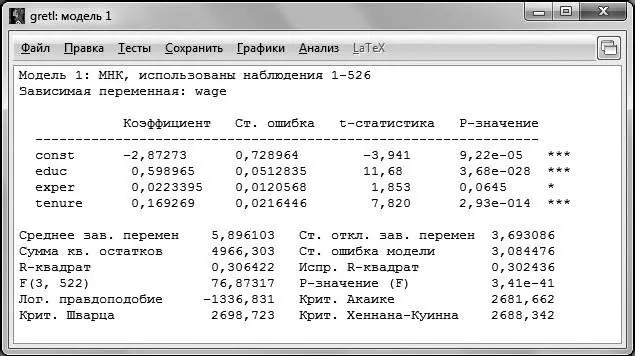
Рис. 2.2
Для того чтобы понимать, какие результаты позволяет получить GRETL, разберем информацию, представленную на распечатке по строкам сверху вниз.
В первой строке указывается метод оценки и количество наблюдений, по которым производилась оценка. Достаточно часто случается, что количество наблюдений, по которым производилась оценка, не совпадает с числом наблюдений в исходной выборке, даже если она не была ограничена. Это может быть связано, например, с наличием пропусков в данных.
Вторая строка напоминает нам о том, какая переменная была выбрана в качестве зависимой.
После двух первых строк следуют подтаблицы непосредственно с результатами оценивания. В первой подтаблице указаны регрессоры, включенные в модель, напротив каждого из них указывается его коэффициент (столбец Коэффициенты ), стандартная ошибка оценки коэффициента (столбец Ст. ошибка ), значение статистики Стьюдента для коэффициента (столбец t-статистика ) и вероятность ошибки I рода (столбец P-значение ). Стоит отметить, что константа тоже является регрессором, и для нее также рассчитываются все указанные характеристики.
Читать дальше

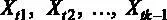 ,
, 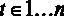 – детерминированные величины.
– детерминированные величины.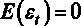 – математическое ожидание ошибок равно нулю,
– математическое ожидание ошибок равно нулю, 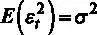 , дисперсия ошибок не зависит от номера наблюдения.
, дисперсия ошибок не зависит от номера наблюдения.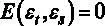 ,
, 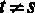 – совместное математическое ожидание ошибок разных наблюдений равно нулю.
– совместное математическое ожидание ошибок разных наблюдений равно нулю.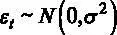 , то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
, то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).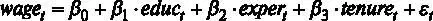 ,
, 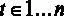 ,
,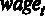 – средний уровень заработной платы в час в долларах,
– средний уровень заработной платы в час в долларах, 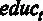 – образование в годах,
– образование в годах, 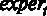 – общий стаж работы в годах,
– общий стаж работы в годах, 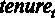 – опыт работы у текущего работодателя, в годах,
– опыт работы у текущего работодателя, в годах, 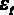 – ошибка регрессии, n – число наблюдений [ файл с данными wage1.gdt ].
– ошибка регрессии, n – число наблюдений [ файл с данными wage1.gdt ].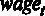 (для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная . Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).
(для этого выделяем ее курсором в списке переменных и нажимаем на стрелку, соответствующую окну Зависимая переменная . Данный способ перемещения переменных справедлив для всех операций с диалоговыми окнами).








![Михаил Гельберт - Физиологические основы поведения и дрессировки собак [Учебное пособие]](/books/406777/mihail-gelbert-fiziologicheskie-osnovy-povedeniya-i-thumb.webp)