Подставив значения энергий в уравнение (19), получим уравнение Бернулли, первое слагаемое которого характеризует динамическое давление, а второе – статическое.
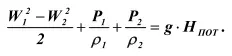 (39)
(39)
Для жидкостей, плотность которых в различных сечениях одинакова, это уравнение после умножения обеих частей на ρ, может быть приведена к более простому виду:
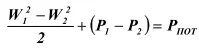 (40)
(40)
Следствием этого закона является то, что сумма динамического и статического давлений в двух сечениях потока с точностью до потерь постоянна, и, например, при сужении потока, динамическое давление возрастает ровно настолько, насколько уменьшается статическое давление.
Сумма статического и динамического давления представляет собой полное давление
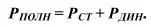 (41)
(41)
На рис. 11. представлен сужающийся трубопровод, в двух сечениях которого установлены трубки Пито, измеряющие полное давление, которое почти одинаково в обоих сечениях, хотя скорость W 2> W 1как это следует из уравнения неразрывности потока.

Рис. 11. Измерение полного давления при помощи трубки Пито
Динамическое давление во втором сечении больше, чем в первом, разница же полных давлений незначительна и равна давлению потерь. Это следует из уравнения Бернулли, так как ровно на столько же падает статическое давление.
Если вместо трубок Пито установить трубки Вентури, которые воспринимают только статическое давление, то мы увидим, что статическое давление в сечении 2 значительно меньше, чем в сечении 1. Определив значение статического давления по трубке Вентури, и вычтя его из полного давления определим динамическое давление в сечении 2 по формуле:
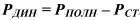 (42)
(42)
Графически соотношение представлено на рис. 10.
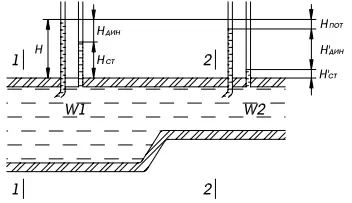
Рис. 12. Соотношение полного, динамического и статического давлений
Аналогичные явления происходят и в газах.
Эффект падения статического давления в струе широко используется в вакуумных преобразователях, например, для запитки вакуумных присосок.
Потери давления
Как мы уже установили, при движении жидкостей и газов возникают потери давления – Р пот.
Они являются следствием двух различных процессов – трения о стенки трубопроводов и завихрений потока.

Рис. 13. Схема определения потерь давления
Поскольку трубопровод неподвижен, то слой, непосредственно примыкающий к его стенке можно считать также неподвижным, следующий слой, расположенный ближе к центру,
перемещается относительно первого с некоторой скоростью, следующий движется с еще большей скоростью и так далее.
Максимальную относительно стенок скорость будет иметь центральный слой.
Если соединить концы векторов скорости плавной кривой, то мы получим годограф скорости (рис. 13), оказывающий распределение скоростей в потоке жидкости или газа.
Для ламинарного течения годограф представляет собой квадратичную параболу, параметры которой зависят от вязкости жидкостей. Если измерить давление по всей длине трубопровода,
то окажется, что давление движущейся жидкости или газа равномерно убывает, поэтому называются потерями по длине.
Экспериментальным путем французский ученый Ж. Пуазейль в 1840 году нашел закон, связывающий потери столба с расходом
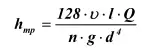 (43)
(43)
где:
υ – кинематическая вязкость,
l – длина трубопровода,
d – диаметр трубопровода,
g – ускорение свободного падения,
Q – объемный расход.
То есть падение давления пропорционально расходу потока Q, (а также его скорости).
Это уравнение может быть представлено в несколько иной записи, которая называется уравнением Вейсбаха-Дарси:
Читать дальше

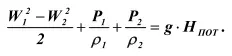 (39)
(39)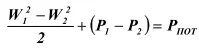 (40)
(40)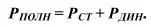 (41)
(41)
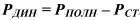 (42)
(42)

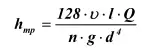 (43)
(43)









