Валентин Арьков - Организация параллельных потоков. Часть 1

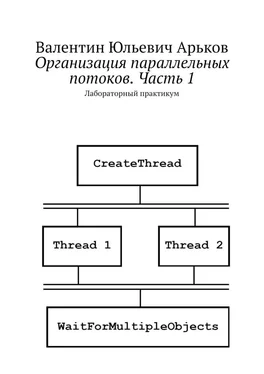
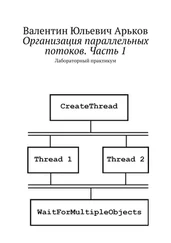
Задание. Выясните, какую точность представления обеспечивают два вещественных типа.

Задание. Проведите эксперименты по численному интегрированию с типом double. Сравните уровень погрешности и время вычислений.

Каждый тип переменной имеет свои пределы возможных значений. Выход в большую и меньшую сторону приводит к потере результатов. К тому же, у нас есть положительные и отрицательные числа.

Задание. Выясните пределы возможных значений для обоих вещественных типов в положительной и отрицательной области значений.

Задание. Составьте тестовые программы и выясните, что происходит при выходе за пределы допустимых значений для обоих вещественных типов.

С увеличением числа прямоугольников погрешность вычислений должна уменьшаться. Однако, при слишком большом числе прямоугольников должно начаться снижение точности и рост погрешности (рис. 6.8). При сложении большого числа с маленьким возникает проблема потери точности. Маленькое число может просто выйти за границы разрядной сетки — это так называемое «обратное переполнение» или «потеря точности / значимости». В нашем случае накопленная сумма значений может оказаться гораздо больше, чем новое прибавляемое значение.

Рис. 6.8. Изменение погрешности вычислений

Можно грубо оценить число прямоугольников, при котором сумма половины значений будет значительно больше, чем одно отдельное, очередное значение f (x). Другими словами, одно значение f (x) должно выйти за пределы разрядной сетки — по сравнению с накопленной суммой.

Более точно можно найти среднее как отношение значения интеграла к интервалу «иксов». Это равносильно замене графика f (x) на прямоугольник с таким же основанием и высотой, соответствующей среднему значению. Площади этих фигур будут равны (рис. 6.9).

Получаем среднее значение аналитически:

f ср= S / (B — A) = 9066,67 / 40 = 227.

Напомним, что наша грубая оценка среднего дала значение 200. Цифры получились достаточно близкими.

Рис. 6.9. Эквивалентный по площади прямоугольник

Задание. Найдите среднее значение f (x) аналитически и сравните с грубой предварительной оценкой.

Представим себе ситуацию, когда сумма S половины значений функции f (x) стала гораздо больше одного отдельного значения f (x), которое к этой сумме надо прибавить:

S>> f (x).

Ситуация потери точности показана на рис. 6.10. В этом примере от всех разрядов f (x) в общую сумму попадает только самый старший, а остальные теряются.

Рис. 6.10. Потеря точности

Примерно оценим сумму половины значений — как среднее f (x), умноженное на половину количества прямоугольников:

S = f ср* N / 2.

Далее можно оценить, при каком числе прямоугольников начинают теряться младшие разряды значения f (x).

Задание. Оцените количество прямоугольников, при котором может начаться потеря точности для переменных типа float и double. Для этого определите, когда будет теряться 1, 2, 3 и т. д. младших разрядов. Оцените время вычислений и тип счётчика цикла.

Задание. Проведите эксперименты, чтобы обнаружить начало потери точности с обоими вещественными типами.

Мы провели подготовительные работы. Можно переходить к экспериментам с параллельными программами. Будем задавать число потоков, равное числу ядер (виртуальных процессоров).

При параллельных вычислениях нужно раздать вычислительные задания разным потокам примерно поровну. Для этого можно использовать метод чередования. Первый поток получает первый отрезок, второй поток — второй отрезок и так далее до максимального номера ядра. Например, до восьмого. Затем мы идём по кругу: первый поток получает девятый отрезок, второй — десятый и так далее. Раздача отрезков продолжается до тех пор, пока не закончатся отрезки.

При организации параллельных вычислений мы просто сообщаем каждому создаваемому потоку его порядковый номер — от 1 до максимального. Затем каждый поток сам находит те значения, которые назначены именно ему.

Задание. Составьте и прогоните параллельные программы для численного интегрирования в соответствии с вариантом задания. Определите показатели эффективности распараллеливания. При возможности доведите программу до потери точности.

Дополнительные эксперименты — это использование части вычислительных ядер, доступных на данном компьютере. В простейшем случае мы запускаем программу, затем она ожидает нажатия клавиши. В этот момент мы задаём Affinity, то есть «соответствие» ядер нашему процессу через Диспетчер задач.