Валентин Арьков - Организация параллельных потоков. Часть 1

Мы объявляем, что входим в критическую секцию:

EnterCriticalSection (&CS).

Все команды, начиная с этого момента, могут выполняться только в одном потоке.

Этап 4. Конец К. С.

Объявляем, что выходим из критической секции

LeaveCriticalSection (&CS).

Дальнейшие команды снова можно выполнять в любом количестве параллельных потоков.

Этап 5. Удаление К. С.

В конце программы удаляем критическую секцию:

DeleteCriticalSection (&CS).

После этой команды мы не больше используем критическую секцию.

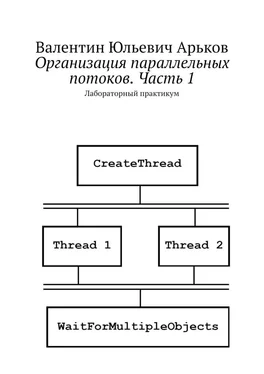
Пример программы параллельного суммирования с использованием К.С. приводится на рис. 5.3.

Рис. 5.3. Использование критической секции

Задание. Составьте программу параллельного суммирования с использованием критических секций (рис. 5.3). Запустите скомпилированную программу на выполнение несколько раз и сравните результаты вычислений.

С помощью критической секции мы обеспечили целостность данных. Теперь программа выполняется без ошибок. Доступ к общей переменной S происходит корректно.

Однако, при этом работа существенно замедлилась. Каждый поток обращает сяк общей переменной и блокирует работу остальных потоков. Поэтому мы не получаем ожидаемого ускорения работы. Необходимо изменить алгоритм так, чтобы потоки работали параллельно, но при этом не затирали чужие результаты. А для нахождения общей суммы придётся задействовать критическую секцию, но это будет небольшая доля всех вычислений.

Задание. Модифицируйте программу (рис. 5.3) так, чтобы получить приемлемое ускорение без потери точности расчетов, используя глобальные и локальные переменные.

При анализе работы параллельных программ используют два основных показателя (рис. 5.4):

— ускорение S p;

— эффективность E p.

В этих формулах использованы следующие обозначения:

p — количество виртуальных процессоров (вычислительных устройств);

T 1 — время выполнения последовательной программы на одном виртуальном процессоре;

T р — время выполнения параллельной программы на рвиртуальных процессорах;

Рис. 5.4. Ускорение и эффективность

Для вычисления этих показателей нужно определить длительность выполнения последовательной и параллельной программ.

В идеальной ситуации ускорение должно быть равно количеству виртуальных процессоров (ядер). Например, для процессора с восемью ядрами можно ожидать ускорение вычислений в восемь раз.

Задание. Определите теоретические значения ускорения и эффективности вашего компьютера и сравните их с полученными в экспериментах.

Мы рассмотрели основы организации параллельных вычислений. В качестве примера задачи для распараллеливания мы использовали нахождение суммы единичек. Теперь мы используем все наши предыдущие наработки и решим более сложную задачу.

Мы будем рассматривать задачу численного нахождения значения определённого интеграла методом прямоугольников. Результаты численных методов должны приближаться к теоретическим (аналитическим).

Мы будем оценивать точность и скорость вычислений, а также показатели эффективности распараллеливания.

В задании необходимо найти значение определённого интеграла (рис. 6.1).

Рис. 6.1. Определённый интеграл

Значения коэффициентов и пределы интегрирования для каждого варианта приведены в Таблице 6.1.

Нулевой вариант используется для демонстрации.

Студент выбирает вариант по последней цифре номера зачётной книжки. Если последняя цифра — ноль, используем вариант 10.

Задание. Укажите в своём отчёте номер варианта и параметры задания.

Ознакомимся с подынтегральным выражением. Построим график этой функции в заданных пределах.

Для построения графика используем возможности пакета Excel (рис. 6.2). Задаём столбец «иксов» и вычисляем столбец «игреков». Затем вставляем точечную диаграмму с гладкими кривыми.

Рис. 6.2. График функции

Задание. постройте график своей функции в заданных пределах.

Для начала попробуем оценить площадь фигуры, то есть площадь под графиком функции f (x) в пределах значений аргумента от —20 до +20.