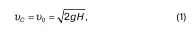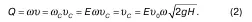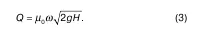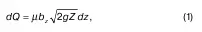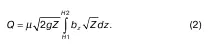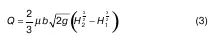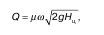М. Бабаев - Гидравлика

Таким образом, имеем резервуар с жидкостью, у которой плотность ρ, из которого через малое отверстие происходит истечение под уровень. Напор Н в центре тяжести отверстия постоянен, что значит, скорости истечения постоянны. Следовательно, движение установившееся. Условием равенства скоростей на противоположных вертикальных границах отверстий является условие d ≤ 0,1Н, где d – наибольший вертикальный размер.

Ясно, что нашей задачей является определение скорости истечения и расхода жидкости в нем.

Сечение струи, отстоящее от внутренней стенки резервуара на расстояние 0,5d, называют сжатым сечением струи, которое характеризуется коэффициентом сжатия

Формулы определения скорости и расхода потока:

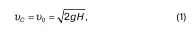
где υ 0называется коэффициентом скорости.

Теперь выполним вторую задачу, определим расход Q. По определению

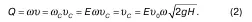
Обозначим Еυ 0= μ 0, где μ 0– коэффициент расхода, тогда

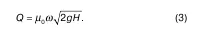
Различают следующие разновидности сжатия:

1. Полное сжатие – это такое сжатие, которое происходит по всему периметру отверстия, в противном случае сжатие считается неполным сжатием.

2. Совершенное сжатие является одной из двух разновидностей полного сжатия. Это такое сжатие, когда кривизны траектории, следовательно, и степень сжатия струи наибольшие.

Подводя итог, заметим, что неполная и несовершенная формы сжатий приводят к росту коэффициента сжатия. Характерной особенностью совершенного сжатияявляется то, что в зависимости от того, под воздействием каких сил происходит истечение.

Отверстие считают малым, когда его вертикальные размеры d < 0,1Н. Большим отверстием будем считать такое отверстие, для которого тот же d> 0,1Н.

Рассматривая истечение через малое отверстие, практически пренебрегли различием скоростей в разных точках сечения струи. В этом случае поступить так же мы не сможем.

Задача та же: определить расход и скорости в сжатом сечении.

Поэтому расход определяют следующим способом: выделяют бесконечно малую горизонтальную высоту dz. Таким образом, получается горизонтальная полоса с переменной длиной bz. Тогда, интегрировав по длине, можно найти элементарный расход

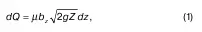
где Z – переменный напор по высоте отверстия, на такую глубину погружен верх выбранной полосы;

μ – коэффициент расхода через отверстие;

b z– переменная длина (или ширина) полосы.

Расход Q (1) можем определить, если μ = const и известна формула b z= f(z). В общем случае, расход определяют по формуле

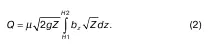
Если форма отверстия прямоугольная, то bz= b = const, интегрировав (2), получаем:

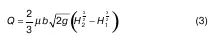
где Н 1, Н 2– напоры на уровнях соответственно у верхней и у нижней кромок отверстия;

Нц – напор над центром отверстия;

d – высота прямоугольника.

Формула (3) имеет более упрощенный вид:

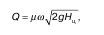
В случае истечения через круглое отверстие пределами интегрирования в (2) служат Н 1= Н ц– r; Н 2= Н ц+ r; Z = Н ц– rcosυ; d z= ρsinυdυ; b z= 2rυsinυ.

Избегая математического излишества, приведем конечную формулу:

Как видно из сравнений формул, особой разницы в формулах для расхода нет, только при больших и малых отверстиях коэффициенты расхода разные

Требуется выяснить вопрос о расходе, если истечение происходит по трубам, соединенным в одну систему, но имеющих разные геометрические данные. Здесь нужно рассмотреть каждый случай отдельно. Приведем некоторые из них.

1. Истечение происходит между двумя резервуарами при постоянном напоре через систему труб, у которых разные диаметры и длина. В этом случае на выходе системы Е= 1, следовательно, численно μ= υ, где Е, μ, υ – коэффициенты соответственно сжатия, расхода и скорости.