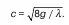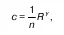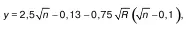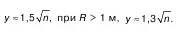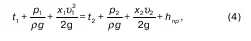3) здесь поток полностью турбулентный; в этой области трубы называются гидравлическими гладкими (шероховатость Δ меньше, чем толщина вязкого слоя δ в, то есть Δ < δ в).
В случае, когда Δ> δ в, труба считается «гидравлически шероховатой».
Характерно, что если для λ лам= f(Re –1), то в этом случае λ гд= f(Re – 0,25);
4) эта область находится на пути перехода потока к подвязкому слою: в этой области λ лам= (Re, Δ/r0). Как видно, коэффициент Дарси уже начинает зависеть от абсолютной шероховатости Δ;
5) эта область называется квадратичной областью (коэффициент Дарси не зависит от числа Рейнольдса, но определяется почти полностью касательным напряжением) и является пристенной.
Эту область называют автомодельной, т. е. не зависящей от Re.
В общем случае, как известно, коэффициент Шези
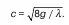
Формула Павловского:
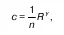
где п – коэффициент шероховатости;
R– гидравлический радиус.
При 0,1 ≤ R ≤ 3 м
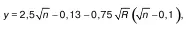
причем при R< 1 м
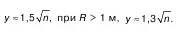
48. Неравномерное движение: формула Вейсбаха и ее применение
При равномерном движении потери напора, как правило, выражаются формулой

где потери напора h прзависят от скорости потока; она постоянна, поскольку, движение равномерное.
Следовательно, и формула (1) имеет соответствующие формы.
Действительно, если в первом случае

то во втором случае

Как видно, формулы (2) и (3) различаются только коэффициентом сопротивления x.
Формула (3) называется формулой Вейсбаха. В обоих формулах, как и в (1), коэффициент сопротивления – величина безразмерная, и в практических целях определяется, как правило, по таблицам.
Для проведения опыта по определению xм последовательность действий следующая:
1) должен быть обеспечен ход равномерности потока в исследуемом конструктивном элементе. Необходимо обеспечить достаточное удаление от входа пьезометров.
2) для установившегося движения вязкой несжимаемой жидкости между двумя сечениями (в нашем случае, это вход с x 1υ 1и выход с x 2υ 2), применяем уравнение Бернулли:
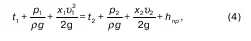
В рассматриваемых сечениях поток должен быть плавно изменяющимся. Между сечениями могло бы произойти что угодно.
Поскольку суммарные потери напора

то находим потери напора на этом же участке;
3) по формуле (5) находим, что h м= h пр– h l, после этого по формуле (2) находим искомый коэффициент
сопротивления

49. Местные сопротивления
Что происходит после того, как поток вошел с некоторым напором и скоростью в трубопровод.
Это зависит от вида движения: если поток ламинарный, то есть его движение описывается линейным законом, тогда его кривая – парабола. Потери напора при таком движении достигают (0,2 × 0,4) × (υ 2/ 2g).
При турбулентном движении, когда оно описывается логарифмической функцией, потери напора – (0,1 × 1,5) × (υ 2/2g).
После таких потерь напора движение потока стабилизируется, то есть восстанавливается ламинарный или турбулентный поток, каким и был входной.
Участок, на котором происходят вышеуказанные потери напора, восстанавливается по характеру, прежнее движение называется начальным участком.
А чему равна длина начального участка l нач.
Турбулентный поток восстанавливается в 5 раз быстрее, чем ламинарный, при одних и тех же гидравлических сопутствующих данных.
Рассмотрим частный случай, когда поток не сужается, как рассмотрели выше, но внезапно расширяется. Почему происходят потери напора при такой геометрии потока?
Читать дальше
Конец ознакомительного отрывка
Купить книгу