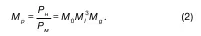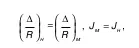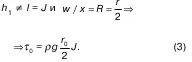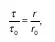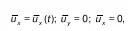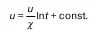М. Бабаев - Гидравлика

Рассмотрим частный случай.

Преобладает влияние сил тяжести, например, при течении через отверстия или водосливы

P = ρgW. (1)

Если перейти к взаимоотношению P ни P ми выразить его в масштабных множителях, то

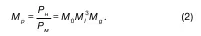
После необходимого преобразования, следует

Если теперь совершить переход от масштабных множителей к самим отношениям, то с учетом того, что l – характерный размер живого сечения, то

В (4) комплекс υ 2/gl называется критерием Фруди, который формулируется так: потоки, в которых преобладают силы тяжести, геометрически подобны, если

Это второе условие гидродинамического подобия.

Нами получены три критерия гидродинамического подобия

1. Критерий Ньютона (общие критерии).

2. Критерий Фруда.

3. Критерий Дарси.

Отметим только: в частных случаях гидродинамическое подобие может быть установлено также по

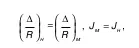
где Δ– абсолютная шероховатость;

R– гидравлический радиус;

J– гидравлический уклон

При равномерном движении потеря напора на длине l heопределяется:

где χ – смоченный периметр,

w – площадь живого сечения,

l he– длина пути потока,

ρ, g – плотность жидкости и ускорение силы тяжести,

τ 0– касательное напряжение вблизи внутренних стенок трубы.

Следует:

Откуда с учетом

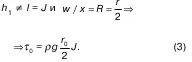
Исходя из полученных результатов для τ 0, распределения касательного напряжения τ в произвольно выбранной точке выделенного объема, например, в точке r 0– r = t это расстояние равно:

тем самым вводим касательное напряжение t на поверхности цилиндра, действующее на точку в r 0– r= t.

Из сравнений (4) и (3) следует:

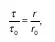
поэтому

Подставив r= r 0– t в (5), получим

Выводы:

1) при равномерном движении распределение касательного напряжения по радиусу трубы подчиняется линейному закону;

2) на стенке трубы касательное напряжение максимально (когда r 0= r, т. е. t = 0), на оси трубы оно равно нулю (когда r 0= t).

R– гидравлический радиус трубы, получим, что

Если рассмотреть плоское движение (т. е. потенциальное движение, когда траектории всех частиц параллельны одной и той же плоскости и являются функции ей двух координат и если движение неустановившееся), одновременно являющееся равномерным турбулентным в системе координат XYZ, когда линии тока параллельны оси OX, то

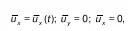
Усредненная скорость при сильно турбулентном движении.

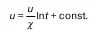
Это выражение: логарифмический закон распределения скоростей для турбулентного движения.

При напорном движении поток состоит в основном из пяти областей:

1) ламинарная: приосевая область, где местная скорость максимальна, в этой области λ лам= f(Re), где число Рейнольдса Re < 2300;

2) во второй области поток начинает переходить из ламинарного в турбулентный, следовательно, увеличивается и число Re;