Журнал «Юный техник» - Юный техник, 2006 № 10

Диаметр винта… 10,0 м

Длина полная… 11,52 м

Высота… З,4 м

Масса пустого вертолета… 0,875 т

Нормальная взлетная масса… 1,680 т

Мощность двигателя… 504 л.с.

Крейсерская скорость… 228 км/ч

Радиус действия… 740 км

Скороподъемность… 400 м/мин

Вместимость… 1 пилот и 4 пассажира

Максимальный потолок… 6000 м

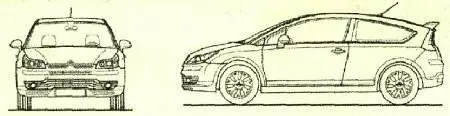
В 2006 г, на автосалоне в Нью-Йорке Citroёn U был удостоен приза за лучший дизайн, победив такие машины, как BMV 3-й серии и европейский вариант Honda Civik . Хотя, стоит сказать, несмотря на новизну, эта переднеприводная модель к тому времени уже успела завоевать множество поклонников во всем мире. Серийно С4 выпускается с кузовами пятидверный и трехдверный хетчбэк, который французы называют словом «купе». Внешне лупе практически полностью повторяет формы Citroen Sport — прототипа С4. Автомобиль выпускается с двигателями объемом от 1,4 до 2 л.

Техническая характеристика:

Тип кузова… хэтчбек

Количество дверей… 3

Длина… 4,270 м

Ширина… 1,770 м

Высота… 1,460 м

База… 2,610 м

Объем двигателя… 1360 cm 3

Мощность… 90 л.с.

Максимальная скорость… 182 км/ч

Снаряженная масса… 1156 кг

Вместимость топливного бака… 60 л

Разгон до 100 км/ч… 14,2 с

Расход топлива… от 5,2 до 8,7 л/100 км

Кратчайшее расстояние между двумя точками — это прямая. Не будем с этим спорить. Но…

Возьмем кирпич и от его края до линии, ему параллельной, приставим к нему две линейки, одну прямую, а другую изогнутую по ломаной линии. Пустив по ним одновременно два одинаковых шарика, можно увидеть, что по кривой линейке шарик попадет в нижнюю точку быстрее. Получается, что кратчайшее расстояние и самый быстрый путь — вещи разные.

Объяснить это можно тем, что, скатываясь по более крутому участку линейки, шарик успевает разогнаться быстрее. Тогда напрашивается вывод, что линейку нужно согнуть под прямым углом. Двигаясь, точнее, падая по вертикали, шарик наберет максимальную скорость, быстро преодолеет горизонтальный участок и скорейшим образом достигнет цели.

Но, как это нетрудно проверить на опыте, такой спуск скорейшим не получается. Вообще же такие опыты наводят па мысль, что линией скорейшего спуска должна быть какая-то особая кривая, соединяющая две точки.

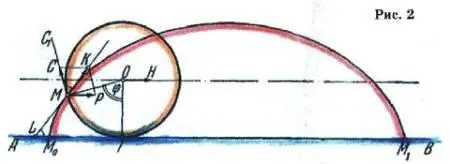
Поиск ее формы оказался делом нелегким и даже привел к созданию нового раздела математики — вариационного исчисления. Когда же эту кривую все же нашли, оказалось, что это давно знакомая всем математикам циклоида — линия, которую описывает точка на ободе катящегося колеса (рис. 2).

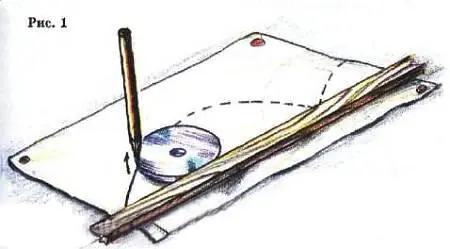
Возьмите, например, старый лазерный диск и как можно ближе к краю проделайте отверстие, в которое входило бы острие карандаша. Положите на лист бумаги линейку и прокатите по ней без проскальзывания диск; на бумаге получится кривая, довольно близкая к циклоиде (рис. 1).

Если бы удалось построить ледяную или снежную гору в форме циклоиды, получился бы замечательный аттракцион. Любые двое санок, одновременно стартующих с разной высоты, спустятся вниз одновременно. Иными словами, под действием силы тяжести они будут проходить разные пути за одно и то же время.

Пока такой горы нет. Она должна иметь высоту 10–15 м и длину около 40 м; во дворе такую не соорудить. Однако гору в форме циклоиды мог бы построить какой-нибудь Луна-парк. Это привлекло бы немало посетителей.

Как продемонстрировать удивительные свойства циклоиды в классе?

В школах города Глазова с некоторых пор можно увидеть приставку к кодоскопу, при помощи которой все особенности циклоиды можно рассмотреть воочию. Здесь по крохотной циклоиде шарики катятся столь медленно, будто земное ускорение уменьшилось во много раз.

Приставка представляет собой несколько направляющих трафаретов из оргстекла толщиной 2–4 мм, уложенных друг на друга (рис. 3).

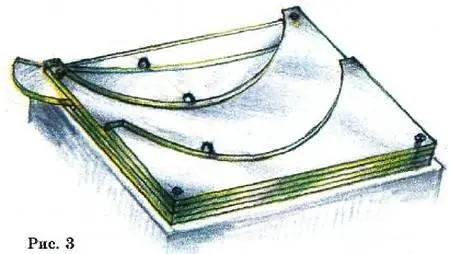
Сверху расположены трафареты двух одинаковых циклоид, а под ними прямая или слегка выгнутая линейка, которую можно поворачивать на оси. Если поставить приставку на кодоскоп, то все, что происходит, станет видно на экране всему классу.