Рудольф Сворень - Ваш радиоприемник

Как, например, определить частоту звука человеческой речи? И вообще, что в данном случае нужно понимать под частотой, если разные по высоте мужские и женские голоса одинаково произносят ту или иную букву?

Мы подошли к очень интересной характеристике звука — его спектральному составу, но прежде чем двигаться дальше, нам необходимо будет провести небольшую подготовительную работу — научиться понимать и самим строить графики.

Повесьте за окном термометр, каждый час отмечайте его показания и затем попробуйте рассказать, как менялась температура в течение суток. Рассказ ваш будет выглядеть примерно так: «В семь часов вечера температура была + 2 градуса, в восемь часов повысилась до +3 градусов, а в девять вновь понизилась до +2. Затем понижение температуры пошло быстрее, в десять часов было ноль градусов, в одиннадцать —3 и так далее». Не правда ли, однообразно? А что, если бы таким способом описывать изменение температуры за неделю или за месяц? Нет, это не годится.

Для того чтобы наглядно показать изменения какой-либо величины — электрического тока, температуры, отклонения маятника или годового производства стали, пользуются специальным рисунком-графиком. Его основа — две перпендикулярные линии, названные осями. Горизонтальную ось размечают в единицах времени, и она похожа на развернутый в длину циферблат часов. Вертикальную ось размечают в единицах той величины, изменение которой нужно описать.

Поскольку мы собираемся описывать изменение температуры, то вертикальную ось нужно будет разметить в градусах так, чтобы она напоминала шкалу обычного термометра. Теперь на поле графика можно делать отметки — против каждого деления времени отмечать соответствующее значение температуры. В результате появится целая серия точек, а когда мы соединим их, то получим сплошную линию, которая как раз и покажет, как меняется температура. Эта линия называется кривой. Так и говорят: «Кривая пошла вниз— температура падает» или «Кривая пошла вверх и пересекла ось времени — температура поднялась выше нуля». Посмотрев на график, на ход кривой, можно сразу определить, какова была температура в различные моменты времени, как она менялась, каким был характер этого изменения.

Подобным же образом можно получить своеобразную летопись звука — график, показывающий, как изменяется давление в какой-либо «озвученной» точке пространства, например, вблизи колеблющейся струны. Только не подумайте, что такой график можно построить с помощью карандаша, бумаги и секундомера — даже при низких частотах весь цикл звуковых колебаний длится какие-то тысячные доли секунды. Для регистрации таких быстрых процессов служит специальный прибор — электронный осциллограф. Именно с его помощью удалось рассмотреть графики самых различных звуков.

На рисунке 11,а, б вы видите два графика одного и того же звука — это нота «ля» 1-й октавы (частота 440 гц), «исполненная» на флейте и кларнете. При построении графиков кверху от оси времени откладывались давления больше нормального (сжатие), книзу от этой оси давление меньше нормального (разрежение). Расстояния до излучателей звука были подобраны так, что амплитуды колебаний, то есть наибольшее сжатие или наибольшее разрежение, оказались одинаковыми. Одинаков период колебаний — это мы оговорили в самом начале, а кроме того, это прекрасно видно из самих графиков.

Внимательно посмотрите на графики. Кроме периода и силы звука, вы обнаружите еще одну его важную характеристику. Это — форма кривой, которая показывает, как меняется звук, с какой скоростью звуковое давление растет, насколько резко уменьшается, «уверенно» ли оно изменяется и т. д. и т. п.

Все эти особенности как раз и отличают одинаковые по частоте звуки, придают им, как говорят музыканты, различную тембровую окраску. Взгляните на график двух различных звуков человеческой речи (рис. 11, в, г). Здесь форма кривой самая главная характеристика, так как именно она отличает эти звуки, например «а» от «о».

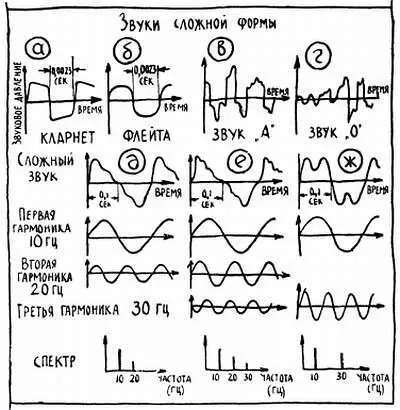
Рис. 11

Вам, наверное, интересно узнать, как наш слуховой аппарат отличает звуки с различными формами кривой. Ведь слушая музыкальные инструменты, мы не вспоминаем ни о каких графиках и вместе с тем прекрасно чувствуем, когда играет рояль, а когда трамбон. Начнем с более простой, но очень похожей задачи.

Представьте, что необходимо точно измерить объем бесформенной гранитной глыбы. Несколько упрощенных методов по какой-то причине не подошли, и вы решили разрезать глыбу на кубики, измерить объем каждого из них, а затем просуммировать все эти объемы. Сначала вы вырежете большой, основной куб, в который войдет основная масса гранита, затем из оставшихся кусков нарежете кубы средней величины и, наконец, не дав пропасть ни одному осколку, ни одной крупинке камня, превратите их в тысячи маленьких кубиков, которые, если их определенным образом сложить, точно воссоздадут сложный рельеф глыбы.