Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Н. — Вот система счисления, которая должна особенно понравиться англичанам. Традиционный английский дюйм легко делится на половинки, четверти, восьмые и т. д. При такой системе счисления относительно просто говорить о 17/64 дюйма.

Л. — Признаюсь, что это никогда не приходило мне в голову. В самом деле можно было бы подумать, что двоичную систему обозначения дробей придумали, чтобы доставить удовольствие тем, кто пользуется этими замысловатыми дюймами и их невероятными долями. А теперь, чтобы у тебя сложилось общее представление о цифровых вычислительных машинах, нам стоит сказать несколько слов о системах памяти.

Н. — Что за любопытное устройство? Для чего оно служит?

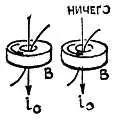
Л. — Запоминающие устройства в вычислительных машинах выполняют ту самую роль, что и бумага, которой мы пользуемся при выполнении расчетов. Во время работы часто приходится записывать промежуточные результаты, чтобы продолжать проводимое вычисление или использовать их позднее. В вычислительной машине благодаря использованию двоичной системы счисления нам нужно лишь зафиксировать в интересующих нас каналах наличие или отсутствие сигнала, что соответствует нулям или цифрам 1. Необходимо сделать так, чтобы результат операции (или данное в условии число) можно было записать.

Н. — Но об этом ты мне уже говорил. Эту задачу можно очень хорошо выполнить с помощью сдвигающего регистра.

Л. — Совершенно верно; сдвигающий регистр содержит триггеры — они могут использоваться в запоминающей системе. В зависимости от состояния, в котором они находятся (опрокинутый триггер или в состоянии покоя), сигналы, даваемые ими, могут соответственно представлять цифры 1 или нули.

Н. — Так, значит в качестве запоминающего устройства мы воспользуемся сдвигающими регистрами?

Л. — Иногда так и делают, но в большинстве случаев такое решение оказалось бы ненужной роскошью. Вполне достаточно простых триггеров. На один из их входов можно подавать под- лежащие запоминанию импульсы, получившие такой импульс триггеры переключатся и останутся в нем до тех пор, пока их не вернут в исходное состояние, т. е. «сбросят на нуль».

Но я хочу рассказать тебе в нескольких словах о более простых запоминающих устройствах. Существует весьма интересный класс запоминающих систем, в которых используются маленькие кольца из ферритов (так называют материалы, состоящие из железа, кислорода и некоторых металлов, которые изготовляются наподобие керамики).

Н. — Ну вот теперь-то я, наконец, услышу объяснение загадочных «тороидов с прямоугольной петлей», о которых я часто слышал, но так толком и не понял, что это такое.

Л. — Именно о них и пойдет у нас речь. Можно сделать ферриты, способные сохранять намагниченность в том или другом направлении при воздействии на них магнитным полем достаточной напряженности.

Предположим, что мы взяли маленькое кольцо, которое я изобразил для тебя на рис. 134…

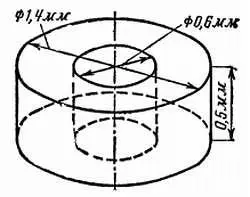
Рис. 134. Ферритовое кольцо, служащее элементом запоминающего устройства благодаря своей способности намагничиваться в одну или в другую сторону.

Н. — Хм, если у тебя нет с собой лупы, тебе придется немало потрудиться, чтобы рассмотреть или найти это кольцо!

Л. — В этом-то и заключается одно из важнейших достоинств системы; малые размеры кольца позволяют сделать запоминающие устройства, содержащие в ограниченном объеме огромное количество элементов. Продернем через отверстие маленького кольца провод и пропустим по нему ток. Если ток превышает некоторое значение (например для нашего кольца 0,7 а), вся система оказывается намагниченной в определенном направлении; при этом силовые линии магнитного поля замыкаются в кольце.

Н. — Значит ли это, что наше кольцо превращается в своеобразный магнит?

Л. — Нет, оно не обладает никаким внешним магнитным полем, так как силовые линии замыкаются внутри феррита. Но мы располагаем средством, позволяющим узнать, в каком направлении намагничено кольцо. Представь себе, что кольцо было намагничено током больше 0,7 а, протекающим по проводу в определенном направлении, а после этого мы посылаем по этому же проводу ток больше 0,7 а, но в другом направлении — кольцо перемагнитится в другую сторону.