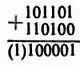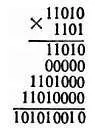Жан-Поль Эймишен - Электроника?.. Нет ничего проще!

Л. — Правильно. Но теперь в твоем числе семь знаков. Если пренебречь последним переносом, у нас останется лишь нуль. Как ты видишь, в результате сложения противоположного В числа и единицы даст нам нечто эквивалентное — В . Следовательно, для получения нужного результата мне достаточно прибавить это число к числу А . Операция имеет следующий вид:

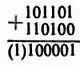
Н. — Я вижу, что в полученном результате слева стоит единица в скобках. Это несомненно появилось вследствие того, что ты не хочешь учитывать последний перенос.

Л. — Совершенно верно. Если теперь прибавить еще одну единицу, то в результате получим 100010. Преобразовав двоичное число в десятичное, получим 34, которое точно соответствует разности 45 и 11.

Н. — Должен признаться, что, не прибегая к двоичной системе счисления, я получил бы верный результат значительно быстрее!

Л. — Ты, может быть. Но электронные машины считают в двоичной системе счисления быстрее, чем в десятичной, даже если учитывать время, необходимое для преобразования.

Н. — Система автоматического счета положительно очень забавна. Не можешь ли ты объяснить мне, как производят умножение?

Л. — На этот раз ты проявляешь исключительную смелость. Схема устройства в самом деле довольно сложная.

Для начала я покажу тебе, как выглядит умножение двоичных чисел по правилам двоичной арифметики. Предположим, что нам нужно перемножить множимое 11010 (или 26) и множитель, равный 13…

Н. — Иначе говоря, 1101.

Л. — О! Ты действительно очень здорово преобразуешь десятичные числа в двоичные. Как ты видишь, наш множитель состоит из следующих слагаемых:

одна единица;

нуль двоек;

одна двойка в квадрате;

одна двойка в кубе.

Следовательно, для получения произведения, мы должны сложить следующие слагаемые:

единица, умноженная на множимое;

нуль, умноженный на это множимое, умноженное на два (иначе говоря, на множимое, к которому справа приписан нуль — 110100);

единица, умноженная на множимое, умноженное на четыре (иначе говоря на множимое, к которому справа приписали два нуля — 1101000);

единица, умноженная на множимое, умноженное на восемь (иначе говоря, на множимое, к которому справа приписали три дополнительных нуля — 11010000).

Следовательно, всю операцию умножения мы можем записать в следующем виде:

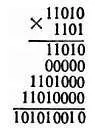
Н. — Теперь, когда я достаточно привык к двоичной системе счисления, твое умножение мне в точности напоминает операцию умножения, которую мне столько раз приходилось выполнять в десятичной системе счисления. Но больше всего меня смущает сложение частичных произведений. Я подозреваю, что выполнить эту операцию с помощью электронных схем окажется ужасно трудно.

Л. — Нет, сложность удается устранить благодаря широкому использованию сдвигающих регистров, о которых ты только что так презрительно отозвался. Вспомни, что эти схемы могут продвигать на один знак записанное число, т. е. умножать его на 2. Для этого в приведенной на рис. 130 схеме достаточно подать управляющий импульс на линию Z . Я полагаю, что теперь ты достаточно натренирован, чтобы смело приступить к ознакомлению с полной схемой умножителя, которую я изобразил на рис. 133. Множимое число мы записали на сдвигающем регистре СР 1 .Множимое расположено так, что справа находятся единица ( а ), а влево от них места занимают двойки ( b ), четверки ( с ), восьмерки ( d ) и т. д. Управляющий сигнал, поступающий в линию Z 1 , продвигает влево число, записанное на сдвигающем регистре CP 1 .

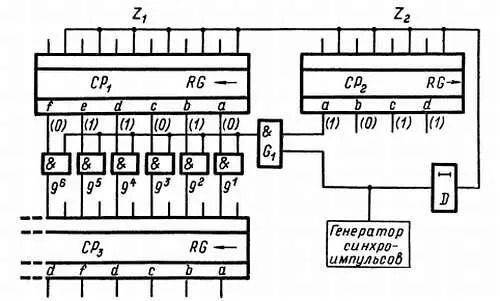
Рис. 133. Полная схема двоичного умножителя, в котором используются три сдвигающих регистра и генератор хронирующих импульсов. Буквой Dобозначен элемент задержки импульсов.

Множитель записан на сдвигающем регистре СР 2 . На этот раз единицы мы разместили на самом левом крае, а вправо от них по порядку записали двойки и т. д. Поступающий в линию Z 2 управляющий сигнал сдвигает записанное число (множитель) тоже влево. Сумма записывается на третьем сдвигающем регистре СР 3 , который работает только Как сумматор. Сдвигающие регистры СР 1 и СР 2 имеют достаточное количество входов и выходов, чтобы операцию можно было выполнить полностью.