Эрл Гейтс - Введение в электронику

Сумматор, учитывающий перенос, называется полным сумматором. Полный сумматор имеет три входа и выходы для суммы и переноса. На рис. 35–21 приведена таблица истинности для полного сумматора. Вход C 1— это вход переноса. Выход С 0— это выход переноса.

Рис. 35–21. Таблица истинности для полного сумматора.

На рис. 35–22 изображен полный сумматор, составленный из двух полусумматоров. Выходы обоих полусумматоров поданы на входы элемента ИЛИ для получения выхода переноса. На выходе переноса будет 1, если на обоих входах либо первого, либо второго элемента исключающее ИЛИ также будут высокие уровни. На рис. 35–23 показаны обозначения полусумматора и полного сумматора.

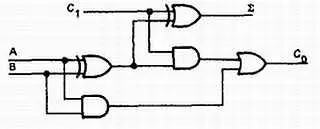
Рис. 35–22. Логическая схема полного сумматора, использующая два полусумматора.

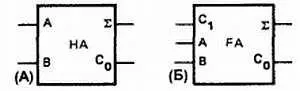
Рис. 35–23. Логические обозначения полусумматора ( А) и полного сумматора ( Б).

Отдельный полный сумматор способен сложить два одноразрядных числа и вход переноса. Для сложения двоичных чисел, имеющих более одного разряда, необходимо использовать дополнительные сумматоры. Вспомним, что когда одно двоичное число складывается с другим, каждый складываемый столбец дает сумму и перенос 0 или 1 в столбец следующего разряда. Для сложения двух двоичных чисел требуется полный сумматор для каждого столбца. Например, для сложения двухразрядного числа с другим двухразрядным числом необходимы два сумматора.

Трехразрядные числа требуют трех сумматоров, четырехразрядные — четырех и т. д. Перенос, создаваемый каждым сумматором, подается на вход сумматора следующего высшего разряда. Поскольку для младшего разряда перенос не требуется, для него используется полусумматор.

На рис. 35–24 изображен 4-разрядный параллельный сумматор.

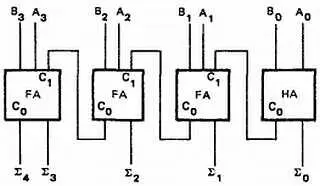
Рис. 35–24. Четырехразрядный параллельный сумматор.

Входные биты младшего разряда обозначены А 0и В 0. Биты следующего разряда обозначены А 1и В 1и т. д. Биты выходной суммы обозначены Σ 0, Σ 1, Σ 2и т. д. Заметим, что выход переноса каждого сумматора соединен со входом переноса сумматора следующего разряда. Выход переноса последнего сумматора является старшим разрядом результата.

Вычитающее устройство

Вычитающее устройство позволяет вычитать два двоичных числа. Для того чтобы, понять, как работает вычитающее устройство, необходимо вспомнить правила вычитания.

На рис. 35–25 приведена таблица истинности, основан нал на этих правилах. Буква D обозначает столбец разности. Столбец заема обозначен буквой В 0.

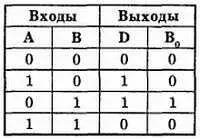
Рис. 35–25. Таблица истинности, составленная с помощью правил вычитания.

Заметим, что на выходе разности ( D ) высокий уровень появляется только тогда, когда входные переменные не равны. Следовательно, разность может быть выражена как исключающее ИЛИ входных переменных. Заем выхода появляется только тогда, когда на А подан 0, а на В подана 1. Следовательно, выход заема является дополнительным к элементу А ИЛИ В .

На рис. 35–26 изображена логическая схема полувычитателя. Она имеет два входа и выдает разность и выход заема. Разность создается элементом исключающее ИЛИ, а выход заема создается элементом И со входами А -и В . Вход А получен путем включения инвертора перед входом А -элемента И.

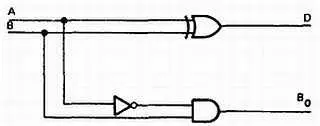
Рис. 35–26. Логическая схема полувычитателя.

Однако полувычитатель не имеет входа заема. Вход заема имеет полный вычитатель. Он имеет три входа и создает разность и выход заема. Логическая схема и таблица истинности полного вычитателя изображены на рис. 35–27. На рис. 35–28 изображены обозначения полувычитателя и полного вычитателя.