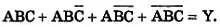Эрл Гейтс - Введение в электронику

ЦЕЛИ

После изучения этой главы студент должен быть в состоянии:

• Объяснить назначение диаграмм Вейча.

• Описать, как использовать диаграммы Вейча для упрощения Булевских выражений.

Цифровые цепи все больше и больше используются в электронике. Область их применения не ограничивается компьютерами, а распространяется на такие приложения, как техника измерений, автоматическое управление и робототехника. Во всех этих приложениях необходимы сложные переключающие цепи, которые формируются на основе пяти основных логических элементов: И, ИЛИ, И-НЕ, ИЛИ-НЕ и инвертора.

Отличительной чертой всех этих логических элементов является то, что они имеют только два рабочих состояния. Это ВКЛЮЧЕНО (1) или ВЫКЛЮЧЕНО (0). При соединении логических элементов между собой для формирования более сложных цепей необходимо получить наиболее простую цепь из всех возможных.

Булева алгебра предлагает метод представления сложных переключающих функций в форме уравнений. Булево выражение является уравнением, которое связывает состояние выхода логической цепи с состоянием ее входов. Диаграммы Вейча обеспечивают быстрый и легкий способ приведения логического уравнения к его простейшему виду.

Диаграммы Вейчаобеспечивают быстрый и легкий метод приведения сложных выражений к их простейшей форме. Они могут быть составлены для двух, трех или четырех переменных. На рис. 33-1 изображено несколько диаграмм Вейча.

Рис. 33-1. Диаграммы Вейчадля двух, трех и четырех переменных.

Для того, чтобы использовать диаграмму Вейча, выполните следующие шаги, которые иллюстрируются на примере.

1. Нарисуйте диаграмму, соответствующую числу переменных.

2. Нанесите на нее логические функции, отмечая их знаком X в соответствующем квадрате.

3. Для получения упрощенной логической функции объедините соседние квадраты, помеченные знаком X в группы по восемь, четыре или два. Продолжайте объединять до тех пор, пока не будут объединены все квадраты, помеченные знаком X .

4. Логически сложите слагаемые (объедините с помощью операции ИЛИ) от каждой петли, одно слагаемое на каждую петлю. (Каждое слагаемое извлекается из диаграммы Вейча и логически суммируется с другими, например ABC + BCD .)

5. Запишите упрощенное выражение.

ПРИМЕР: Упростите АВ + А -В + АВ -.

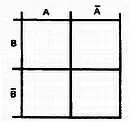
Шаг 1.Нарисуем диаграмму Вейча. Мы имеем две переменных А и В , поэтому используем таблицу для двух переменных.

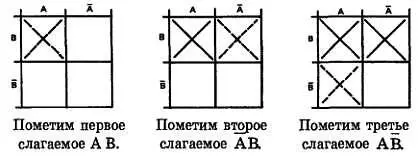
Шаг 2.Нанесем логические функции, помечая их знаком X в соответствующем квадрате.

Шаг 3.Объединим соседние квадраты, помеченные знаком X , в наибольшие возможные группы. Проанализируем диаграмму — какая возможна наибольшая группа? Наибольшая возможная группа состоит из двух квадратов.

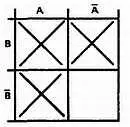
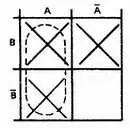
Одна из возможных групп показана штриховой линией.

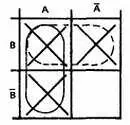
Другая возможная группа на этой диаграмме показана штриховой линией.

Шаг 4.Логически сложим эти группы (операция ИЛИ):

или А , или В = А + В.

Шаг 5.Упрощенным выражением для АВ + А - В + АВ -= Y является А + В = Y , что получено из диаграммы Вейча.

ПРИМЕР: Найдите упрощенное выражение для

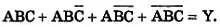
Шаг 1.Нарисуем диаграмму Вейча для трех переменных.

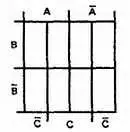
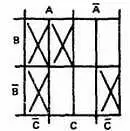
Шаг 2.Пометим знаком X логические функции каждого слагаемого на диаграмме Вейча.