В Бессонов - Радиоэлектроника для начинающих (и не только)

5) При X L= X C или ω 0∙ L =1/ ω 0∙ C

6) Первый вариант ( рис. а ) — согласное соединение обмоток.

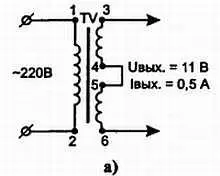
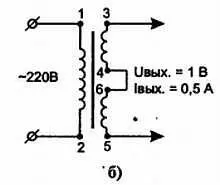
Второй вариант ( рис. б ) — встречное соединение обмоток.

1) S= Δ I/Δ U= 5/(0,6–0,4) — 5/0,2 = 25 мА/В

2, a )R = 100 Ом. Общее сопротивление цепи для прямого тока рано 20 + 100 = 120 Ом, при этом сопротивление резистора R составляет 100/120 = 0,83 от сопротивления всей цепи. Тогда U Rmax= E m∙0,83 = 2 В.

Для обратного тока общее сопротивление цепи равно 300000 + 100 ~= 300000 Ом, а напряжение на выходе (на резисторе) равно 2,4∙100/100000 ~= 0, т. е. U Rmin ~= 0.

б) R = 300 кОм. U Rmax= 2,4 В. U Rmin= 1,2 В.

3) I Б= I Э— I К= 5–4,7 = 0,3 мА.

4) I Б= I Э— I К= 18–17 = 1 мА. h 21Э= Δ I К/Δ U Б= 17/1 = 17

5) h 21Э= h 21б/(1- h 21б)= 0,95/0,05 = 19

1) Для нахождения характера изменения тока в цепи, схема которой приведена на рис. 5.22,а, воспользуемся следующими рассуждениями. В те полупериоды синусоидального напряжения, когда диод находится в прямом включении, падение напряжения на нем согласно рис. 5.22, б не превышает 0,5 В и пренебрежимо мало по сравнению с приложенным ко всей цепи напряжением. Поэтому ток в цепи определяется только сопротивлением резистора нагрузки, т. е.

I= U вх/ R н= 160/5000 = 0,032 А = 32 мА.

В те полупериоды, когда диод находится в обратном включении, сила тока в цепи согласно рис. 5.24, в не превышает 10 мкА. Таким образом, сила тока в нагрузке на рис. 5.22, а представляет собой сигнал, состоящий из двух полуволн с амплитудами 32 мА и 10 мкА. Осциллограмма силы тока приведена на рисунке, причем для наглядности полуволны изображены в разных масштабах.

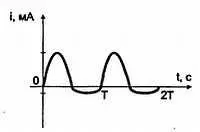
2) В каждый полупериод синусоидального напряжения ток проходит через два диода и нагрузочный резистор R н. Таким образом, общее сопротивление нагрузки R но, подключенной к вторичной обмотке трансформатора, равно 120 + 10 + 10 =140 Ом. Тогда сила тока через сопротивление нагрузки равно:

I m = U 2m∙ n тр/ R но= 140∙0,1/140 = 0,1 А.

3) U Н. пер= 12,45 В, U Н. пост= 19,6 В, К пост= 0,98, K пер= 0,62, К пост/ K пер= 1,58. Коэффициент передачи по переменному току K пер= U Н. пер/ U Вх. перопределяется делителем напряжения, одним из плеч которого является резистор R , а другим — параллельное соединение резистора R ни емкостного сопротивления конденсатора Х с= 1/ ω∙ С; коэффициент передачи по постоянному току определяется делителем R, R н.

4) В задаче приведена статическая характеристика стабилизатора, т. е. зависимость выходного напряжения от входного. По своему функциональному назначению стабилизаторы отличаются тем, что в них достигается неизменность выходного напряжения в широком диапазоне изменения входного, т. е. их статическая характеристика приближается к вольт-амперной идеального источника напряжения с R вн= 0. Определенная сложность при решении задачи заключается в том, что коэффициент стабилизации представляет собой дифференциальную величину и от вас требуются навыки по нахождению производной. Коэффициент стабилизации находится из следующего соотношения:

K ст= U н/ U вх∙d U вх/d U н

Зависимость U н= f ( U вх) задана в условии в виде линейной функции, следовательно, ее производная равна постоянной величине d U вх/d U н= 100. Таким образом, коэффициент стабилизации в данном случае равен:

K ст= [(0,01∙ U вх+ 10)/ U вх]∙100

где U вх— в вольтах.

Подставляя в последнее выражение заданные в условии значения входного напряжения, получаем K ст= 101; 21; 11.

5) Изменение напряжения на выходе стабилизатора Δ U ст= Δ I ст∙ R д= 16∙10 -3В. Тогда относительное изменение напряжения на выходе стабилизатора равно