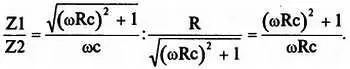В Бессонов - Радиоэлектроника для начинающих (и не только)

1. Обмотка с ферромагнитным сердечником, по которой может проходить электрический ток.

2. Внесистемная единица магнитной индукции.

3. Способность веществ проводить постоянный электрический ток.

4. Характеристика магнитного поля.

5. Величина, характеризующая изменение магнитной индукции поля в веществе.

7. Энергетическая характеристика электростатического поля.

9. Датчик температуры, действие которого основано на возникновении термоэдс.

11. Накопитель электрической энергии.

13. Система из двух или более проводников, разделенных диэлектриком.

15. Совокупность явлений, связанных с действием магнитного поля.

16. Диэлектрик, длительно сохраняющий наэлектризованное состояние.

17. Основная характеристика магнитного поля.

18. Образование ионов и свободных электронов из атомов и молекул.

19. Класс физических величин, к которым относится напряженность электрического поля.

20. Американский ученый-самоучка, впервые наблюдавший термоэлектронную эмиссию.

24. Траектория электрона, движущегося вокруг ядра атома.

25. Намагниченный ферромагнетик.

26. Один из электродов транзистора.

27. Система двух равных и противоположных по знаку электрических зарядов.

28. Единица электрической проводимости в СИ.

29. Прибор, пропускающий электрический ток только в одном направлении.

31. Устройство для электрического соединения или разъединения цепей (состоящее обычно из вилки и розетки).

32. Области магнетика, самопроизвольно намагниченные до насыщения.

37. Источник электрического поля, связанный с материальным носителем.

38. Единица электрической емкости в СИ.

1, а )При подключении вольтметра к перегоревшей лампе он покажет напряжение сети. Когда вольтметр подключен к исправной лампе, его показания будут равны нулю.

1,б ) При подключении неизолированных концов провода к выводам сгоревшей лампы, все лампы гирлянды загорятся.

2) Пренебрегая потерями в источнике питания, напишем уравнение, определяющее мощность, рассеиваемую в цепи: 25 I 2+ 5 = 30 I. Мы получили полное квадратное уравнение (а х 2+ Ь х+ с = 0, где а = 25, b = -30, с = 5) 25 I 2— 30 I+ 5 = 0. Решив это уравнение относительно I , получим значения токов, при которых на реостате R1 рассеивается мощность, равная 5 Вт: I 1= 1 А, I 2= 0,2 А.

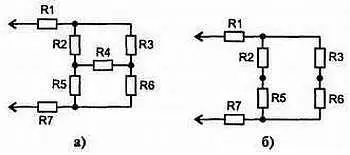
3) Эту схему можно нарисовать по-другому (см. рис. а ). Если подключить к зажимам схемы источник напряжения, то можно заключить, что на резисторе R4 напряжение равно нулю и сила тока через него равна нулю. Тогда схему можно перерисовать так (см. рис. б ). А сопротивление этой цепи легко рассчитать.

Ответ: R = 3 Ом.

4) В схеме а) — лампы 1,2: в схеме б) — лампа 4: в схеме в) — лампа 3: в схеме г) — лампа 4.

5) Общее сопротивление параллельно соединенных резисторов R5 и R6 составляет 200 Ом, т. е. равно сопротивлению резистора R3. Если это так, то суммарная сила тока, протекающая через резисторы R4, R5, R6, равна 1 А, а общая сила тока в цепи — 3,75 А.

6) а) 6 Ом; б) 18 Ом; в) 4 Ом; г) 12 Ом.

1) Мощность тока в паяльнике Р= U∙ I= 220∙0,9 = 198 Вт; сопротивление обмотки паяльника R= U/ I= 220/0,9 = 244 Ом.

2) Из формулы вычисления мощности Р= U 2/ Rнаходим R= U 2/ P= 220 2/100 = 484 Ом.

3) Из формулы R = U 2/P видно: чем больше знаменатель дроби, тем меньше частное от деления. Отсюда вывод: лампа мощностью 100 Вт имеет меньшее сопротивление.

4) При последовательном соединении элементов R и С общее сопротивление цепи равно:

Z1= √[ R 2+ (1/ ω∙ C) 2],

а при параллельном соединении

Y2= ([(1/ R) 2+ ( ω∙ C) 2]

Отсюда Z2= 1/ Y2 = R/√[( ω∙ Rc) 2+ 1]

Тогда

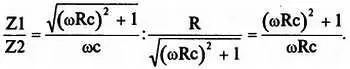
При f = 10 6Гц, R = 1 кОм, С = 1 мкФ, Z1/ Z2= ω∙ Rc = 2π f∙ Rc >> 1, т. е. Z1>> Z2