Карлос Касадо - Вселенная работает как часы. Лаплас. Небесная механика.

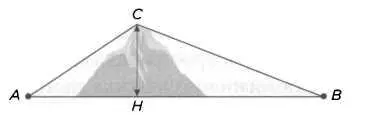
При помощи теодолита или, для большей точности, повторительного круга Борда они могут измерить углы, с которых можно наблюдать вершину горы в обоих городах, то есть угол А треугольника АСН и угол В треугольника ВСН. При помощи барометра, измеряющего давление по отношению к высоте, можно узнать высоту горы, или расстояние между Н и С. Применяя к этим данным правила тригонометрии, делаем вывод, что тангенс угла А равен высоте НС, разделенной на расстояние АН. Тангенс угла В равен высоте НС, разделенной на расстояние ВН. Выделив неизвестное из АН и ВН в обоих выражениях и сложив их, получаем:

AB = AH + HB = HC/tg(A) + HC/tg(B),

то есть расстояние между городами А и В.

Однако введение новых единиц измерения столкнулось с трудностями. Народ не понимал значения этих странных греческих и латинских префиксов — кило- и санти-. Пришлось подключать пропаганду. В сентябре 1801 года был принят закон, запрещающий использование других систем измерения, помимо метрической, но действовал он только на бумаге. Через несколько лет, в 1812 году, Франция вернулась к традиционным единицам. Один из поэтов высмеивал метрическую систему: «Неужели для того, чтобы выпить стакан вина, отрезать локоть материи или починить часы, действительно необходимо измерить дугу меридиана?» Однако хотя метрическая система не была признана в самой Франции, завоевания Наполеона помогли распространить ее за пределы страны. В Нидерландах и Бельгии метрическая система установилась в 1820 и 1830 годах соответственно, хотя сама Франция, эту систему запатентовавшая, в это время все измеряла по старинке. Метрическая система будет применена в ней лишь в 1840 году, когда Шарль Эмиль, сын Лапласа, станет президентом комиссии, которая предложит вернуться к метрической системе, как этого хотел его уже покойный отец. Время подтвердило правоту Лапласа. Германия ввела эту систему в 1868 году, а Соединенные Штаты Америки и Великобритания все еще сохраняли прежние единицы измерения.

Бесспорно, гармонизация мер и весов является одним из важных достижений революции. Метр стал даром французских ученых всем людям и на все времена; и ценность этого дара огромна и сегодня, спустя более чем два века.

Между 1789 и 1794 годами вся образовательная система старого режима была разрушена, религиозные коллежи опустели. В 1795 году началось формирование новых институтов общественного образования, что выразилось в создании Центральной школы государственных работ, сегодня известной как Политехническая. Именно из этой высшей школы, направленной на изучение инженерного дела, вышли гражданские и военные инженеры, а также самые блестящие ученые Франции. Настоящим создателем школы был Монж, однако он отошел в тень Лапласа, который сам не преподавал, но разрабатывал программы обучения — Лаплас в конце своей карьеры был назначен в школе экзаменатором. Здесь развивалось практическое обучение, важное в годы военных кампаний и развития промышленности. Однако помимо исключительно прикладных наук (металлургия, фортификация, строительство мостов и картография), в школе также уделялось большое внимание физике и математике.

В это же время была создана Высшая нормальная школа, предназначенная для обучения нового педагогического состава для всех учреждений обновленной системы образования. Школа была торжественно открыта 1 плювуаза II года (20 января 1795 года) в амфитеатре музея естественной истории. До 30 флореаля того же года Лагранж и Монж, как и другие ученые, вели уроки для школьных учителей будущих граждан нации. Около 1200 слушателей, малообразованных, но воодушевленных, изучали здесь элементарную математику. Проект Высшей нормальной школы просуществовал лишь четыре месяца, но его влияние ознаменовало новую эру в системе образования Франции.

Амфитеатр музея едва мог уместить всех желающих присутствовать на лекции Лапласа. Он поставил себе цель представить за десять уроков самые важные открытия в области математики. Первые восемь были посвящены арифметике, алгебре, уравнениям, элементарной и аналитической геометрии. Темой девятого должна была стать новая метрическая система, а десятого — теория вероятностей. На этом последнем уроке Лаплас представлял одну из тем, над которой он работал с Кондорсе: как можно применять математику в общественных целях путем расчета вероятностей. Спустя два десятилетия математик вновь открыл план своего урока о вероятностях и опубликовал его сначала в качестве введения к одной из своих самых важных работ — «Аналитическая теория вероятностей», а затем — в труде «Опыт философии теории вероятностей», который мы рассмотрим в главе 5.