Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

В начале XX века многие математики были уверены, что для решения проблемы парадоксов теории множеств достаточно добиться верной формулировки ее аксиом. Первый шаг в этом направлении сделал немецкий математик Эрнст Цермело (1871-1953). В 1919 году немецкий математик Абрахам Френкель (1891-1965) усовершенствовал систему аксиом Цермело, добавив к ней неучтенные прежде необходимые аксиомы. Сегодня она называется системой Цермело — Френкеля, а в специальной литературе по теории множеств обозначается аббревиатурой ZF. Эти аксиомы составляют стандартные формулировки теории множеств и позволяют решить все известные парадоксы. Слово «известные» было добавлено чешским математиком Куртом Гёделем (1906-1978), который доказал, что не существует безошибочного способа гарантировать, что система аксиом не содержит парадоксов. Таким образом, хотя в глубине души математики убеждены, что ZF не приведет к логическим противоречиям (и действительно, с 1919 года они не были выявлены), не существует математически точного доказательства того, что они никогда не возникнут.

Каждая сторона этого памятника в Галльском университете посвящена профессору, работавшему здесь. Сторона слева — Виктору Клемпереру (1881-1960), профессору философии, сторона справа — Кантору.

Сторона памятника, посвященная Кантору. Под изображением ученого высечено равенство x = X02 . а внизу — фраза из его работы 1883 года: «Сущность математики состоит в ее свободе».

Перечислим аксиомы Цермело — Френкеля.

1. Два множества равны, если в них одинаковое количество членов.

2. Существует пустое множество.

3. Если даны х и y, всегда существует пара, состоящая из них обоих.

4. Объединение двух или больше множеств также является множеством.

5. Существует по крайней мере одно бесконечное множество.

6. Только свойства, которые можно выразить исходя из остальных аксиом, могут быть использованы для определения множества.

7. Если дано произвольное множество, всегда существует множество, образованное его частями (см. главу 5).

8. Если дана семья — конечная или бесконечная — непустых множеств (то есть каждое из них содержит как минимум один член), всегда существует множество, которое содержит по члену из каждого множества этой семьи (см. рисунок на следующей странице).

9. Ни одно множество не является членом самого себя.

Аксиома 9 подразумевает, что универсального множества не существует, потому что оно содержало бы само себя, а аксиома это запрещает. Действительно, если записать аксиомы подходящим символическим языком, то можно доказать, что, исходя из аксиомы 6, универсальное множество даже не может быть определено. Парадокс Кантора возникает, когда речь заходит именно о мощности универсального множества. Но если его не существует, то нет и парадокса.

Парадокс Рассела связан с множеством F, образованным всеми множествами, которые не являются членами самих себя. Но аксиома 9 гласит, что все множества соблюдают условие, определяющее F; следовательно, F будет множеством всех множеств. Но поскольку оно и само является множеством, по аксиоме 9, то не может существовать (на самом деле, как и в случае с универсальным множеством, можно доказать, что даже нельзя определить теоретически). А раз оно не существует, то не будет и парадокса Рассела.

Парадокс Бурали-Форти решается аналогичным способом — через доказательство того, что множества всех ординальных чисел не существует.

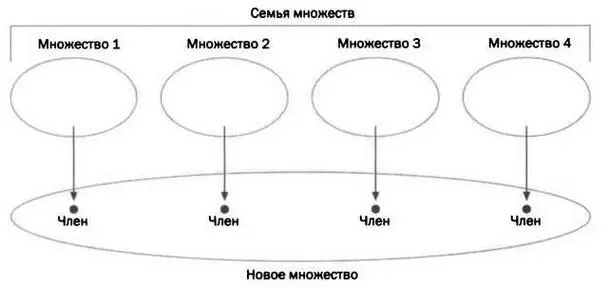
Схема, объясняющая аксиому выбора. От каждого множества выбирается по члену и из них формируется новое множество.

Несмотря на успех ZF, в XX веке были предложены и другие системы аксиом для теории множеств. Обычно они обозначаются инициалами ученого, который сформулировал их первым. Так, существует система NBG (Джона фон Неймана, Пола Бернайса и Курта Гёделя) и система МК (Роберта Ли Морза и Джона Лероя Келли). Эти системы не равнозначны. Это не просто разные формулировки одной и той же идеи — различия лежат в самих их основаниях. В частности, не все системы предлагают одно и то же решение парадоксов. Самой популярной система ZF стала отчасти потому, что она же и самая простая, но и у других есть свои сторонники. Прочие системы сводятся к тому, что множеств, которые Кантор называл «недоступными», не существует, как в ZF, либо, как в NBG и МК, существование «недоступных» множеств допускается, но провозглашается, что они подчиняются правилам, отличным от других множеств.