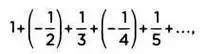Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

В нашем случае необходимо рассматривать последовательности, состоящие из бесконечного количества чисел, различных между собой.

Возьмем множество рациональных чисел. Очевидно, что π как иррациональное число не принадлежит к этой группе, и тем не менее его можно представить в виде последовательности рациональных чисел. Мы можем найти такую последовательность, состоящую исключительно из рациональных чисел, что по мере продвижения вперед будем получать числа все ближе к π. В примере из предыдущей главы последовательность 3,1; 3,14; 3,141; 3,1415;... получается путем прибавления к каждому последующему числу одного знака после запятой в числе π.

Это справедливо и для любого другого иррационального числа: мы всегда сможем приблизиться к нему через последовательность рациональных чисел. То же распространяется и на рациональные последовательности. Например, если мы возьмем число 0,75, то последовательность 0,751; 0,7501; 0,75001; 0,750001;... будет все ближе подходить к нему. То есть приближение любого вещественного числа возможно через последовательность рациональных чисел (что по сути и является решением Кантора задачи о континууме).

Математики XIX века, корпевшие над логическим обоснованием исчисления и открывшие ряды, то есть бесконечные суммы, выработали свои правила, которые существенно отличаются от тех, которые используются для привычных конечных сумм. В 1854 году немецкий математик Бернхард Риман (1826-1866) доказал: некоторые бесконечные суммы не обладают коммутативностью; другими словами, они могут быть реорганизованы так, что получится другой результат. Например, в ряде

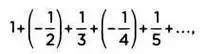
сумма которого равна 0,6931471..., слагаемые могут быть распределены так, чтобы получился любой желаемый результат.

Георг Фридрих Бернхард Риман, 1862 год.

Если Р — произвольное множество чисел, то производным от Р множеством Кантор называл группу чисел, которые можно аппроксимировать через последовательности, состоящие из элементов Р. Он обозначил такое множество Р. Если Q — множество рациональных чисел, то предыдущий пример показывает, что Q' = R, где R обозначает множество всех вещественных чисел.

Труды Кантора — прекрасный плод математического гения и одно из высочайших достижений человеческого интеллекта.

Давид Гильберт, немецкий математик

В статьях начала 1870-х годов Кантор представлял определение производного множества в терминах потенциально бесконечных множеств. Но сама структура Q' отсылает к актуальной бесконечности, поскольку Q заключает в себе все рациональные числа. С другой стороны, определение Q' приводит нас к последовательностям и к определению вещественных чисел. Рассмотрим теперь, как проблема тригонометрических рядов подтолкнула Кантора к двум основным темам его последующих математических исследований — к актуальной бесконечности и к задаче о континууме.

Теперь возьмем множество Р, состоящее исключительно из чисел 0, 1 и 2. Множество Р, по определению Кантора, содержит все числа, которые можно аппроксимировать посредством последовательностей, состоящих из бесконечных различающихся элементов Р. Очевидно, что бесконечных и различающихся элементов Р не существует, поскольку их в этом множестве всего три.

Так как создать даже одну последовательность элементов Р невозможно, то в Р ничего нет. В этом случае, как писал Кантор, Р аннулируется. Сегодня мы бы сказали, что Р — пустое множество, то есть в нем нет составляющих, но мы оставим выражение Кантора. Чтобы понять условие единственности, найденное Кантором, вернемся к примеру производного Q' и убедимся, что оно также является множеством чисел, а значит, мы можем рассчитать его производное. Кантор записывал производное от производного Q как Q". Поскольку оно тоже является множеством, то мы можем рассчитать и его производное, которое будет записано как Q (3); а его производное — как Q (4), и так далее.

В случае с Q эта цепь производных не дает интересного результата, потому что Q', Q", Q (3), Q (4),... являются множествами вещественных чисел, а значит, продолжая получать их производные, мы не достигнем ничего нового. Но существуют такие множества Р (о них мы не будем говорить подробно), производные которых Р', Р", Р (3), Р (4)... являются разными множествами или такими, что в конце концов процесс получения производных Р', Р", Р (3), Р (4)... аннулируется. Например, можно найти множество Р, для которого Р состоит из чисел 0, 1 и 2. В этом случае Р", производное от Р', аннулируется. В других случаях аннулируется Р' в третьих — Р (3)или Р (4)и так далее. Разумеется, для Q этот процесс никогда не закончится, потому что на всех его этапах мы получим множество вещественных чисел R. Условие единственности, найденное Кантором, состоит в следующем: если Р — множество абсцисс точек прерывания периодического графика, то для того чтобы был всего один способ разложить его в тригонометрический ряд, достаточно, чтобы процесс Р', Р", Р (3),Р (4),... рано или поздно заканчивался. Так Кантор смог ясно и точно изложить условие, обеспечивающее единственно возможный способ разложения на ряд Фурье, и решил задачу, поставленную перед ним Гейне в 1869 году.