Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Лекция Римана, прочитанная им в 1854 году, ознаменовала собой тектонический сдвиг в понимании геометрии, возникающий в результате низвержения постулата о параллельных — Риман дал описание всеобъемлющей теории, включающей как Евклидовы, так и не Евклидовы идеи. Ключевой концепцией, лежавшей в основе теории Римана, была кривизна пространства. Когда поверхность имеет нулевую кривизну, она является плоской, или евклидовой, и тогда выполняется все, что получено в «Началах». Когда же поверхность искривлена, то есть имеет положительную или отрицательную кривизну, она — неевклидова, и применительно к ней написанное в «Началах» неверно.

Простейший способ понять, что такое кривизна, учит нас Риман, — рассмотреть то, что происходит с треугольниками. На поверхности нулевой кривизны сумма углов треугольника — 180 градусов. На поверхности положительной кривизны эта сумма превышает 180 градусов. На поверхности отрицательной кривизны углы треугольника дают в сумме менее 180 градусов.

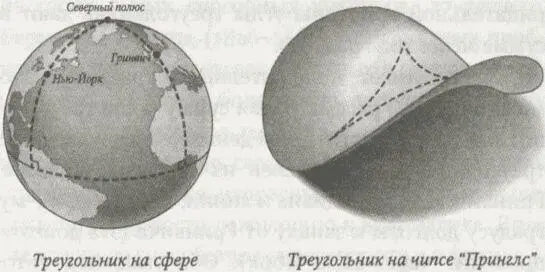
Сфера имеет положительную кривизну. Это можно понять, рассматривая сумму углов треугольника в левой части приведенного ниже рисунка: треугольник там составлен из отрезков экватора, Гринвичского меридиана и линии, идущей по 73-му градусу долготы к западу от Гринвича (эта долгота проходит через Нью-Йорк). Оба угла, под которыми линии долготы пересекают экватор, равны 90 градусам, так что сумма всех трех углов должна быть больше 180 градусов.

А поверхности какого типа имеют отрицательную кривизну? Другими словами, где искать те треугольники, углы которых в сумме дают меньше 180 градусов? Откройте пачку картофельных чипсов «Принглс», и вы поймете где. Нарисуйте треугольник на седловой части чипса (для чего можно использовать тюбик с нежной французской горчицей) — треугольник будет выглядеть как «вогнутый» в сравнении с «выпуклым» треугольником, который мы наблюдали на сфере. Ясно, что его углы в сумме дают менее 180 градусов.

Поверхность отрицательной кривизны называется гиперболической. Итак, поверхность чипса «Принглс» — гиперболическая. Впрочем, чипс — это всего лишь первый шаг к пониманию гиперболической геометрии, потому что у него есть край. Стоит только показать математику край, как он тут же захочет выйти за его пределы.

Можно посмотреть на это и другим способом. Проще всего представить себе поверхность нулевой кривизны без края: взять хотя бы ту страницу, что сейчас перед вами, разгладить ее, положить на стол, а потом продолжить по всем направлениям до бесконечности. Если бы мы жили на подобной поверхности и отправились на прогулку вдоль прямой линии в любом направлении, то никогда не добрались бы до края. Аналогичным образом, у нас есть очевидный пример поверхности положительной кривизны без края: это сфера. Если бы мы жили на сфере, то могли бы идти, никогда не останавливаясь и нигде не встречая края. (Конечно, мы и в самом деле живем на том, что представляет собой грубое приближение к сфере. Если бы Земля была совершенно гладкой, без всяких океанов и гор, встающих у нас на пути, и мы бы отправились в путь, в конце нашего путешествия мы снова вернулись бы к исходной точке — на самом деле мы двигались бы по окружности.)

А как же выглядит поверхность отрицательной кривизны без края? Она не может выглядеть как чипс, потому что если мы бы жили на чипсе «Принглс» размером с Землю и начали бы шагать в одном направлении, то в конце концов свалились бы за край. Математики долго гадали, как могла бы выглядеть «бескрайняя» гиперболическая поверхность — такая, по которой можно было бы путешествовать так далеко, как только захочется, и никогда не достигать края, но которая при этом не теряет своих гиперболических свойств. Понятно, что такая поверхность должна быть постоянно изогнута как чипс; так может, попробовать склеить ее из множества чипсов указанной формы? Увы, так у нас ничего не получится, потому что чипсы «Принглс» плохо состыковываются один с другим, а если заполнять образующиеся пустоты какой-то другой поверхностью, то эти добавленные области не будут гиперболическими. Другими словами, чипсы позволяют представить себе лишь локальные гиперболические свойства. Вещь, которую необычайно сложно представить — и которая требует напряжения мысли у даже самых блестящих математических умов, — это гиперболическая поверхность, которая продолжается без конца и без края.