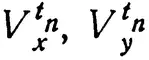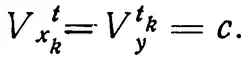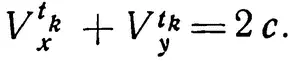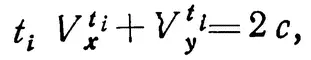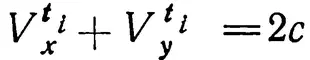Виолетта Гайденко - Западноевропейская наука в средние века - Общие принципы и учение о движении

Главным результатом математических вычислений, проводившихся в Мертон-колледже, были формулировка и доказательство фундаментальной кинематической теоремы, которая приравнивает (в отношении пути, пройденного за определенный отрезок времени) равноускоренное движение равномерному, скорость которого равна скорости равноускоренного движения в средний момент времени последнего. В современной символической записи мертонская теорема средней скорости будет выглядеть следующим образом:

1) S = ½ ∙ V f∙ t — для случая ускорения от состояния покоя;

2) S = (v 0+ (v f– v 0)/2)/t — для ускорения от начальной скорости v 0.

где S обозначает проходимое расстояние, v f— конечную скорость, a t — время ускорения.

Рассмотрим вначале доказательство Суайнсхеда, а затем доказательство Хейтсбери.

а) Доказательство Ричарда Суайнсхеда

Выше приводилось одно из мертонских доказательств теоремы о среднем градусе, принадлежащее Суайнсхеду. Доказательству в трактате Суайнсхеда предпосланы формулировка и разъяснение самой теоремы: «Всякая широта движения, равномерно приобретаемая или утрачиваемая, соответствует своему среднему градусу… Я говорю, что широта, которая приобретается, соответствует своему среднему градусу в том смысле, что ровно столько же будет пройдено посредством той широты, таким именно образом приобретаемой, сколько и посредством ее среднего градуса, если в продолжение всего (totum) времени движение будет происходить с тем средним градусом» [89]. Чтобы доказать это утверждение, Суайнсхед предлагает проделать мысленный эксперимент (излагая его рассуждение, мы постараемся воспроизвести основную идею, не следуя буквально способам ее выражения). Предположим, что тело x движется равноускоренно в течение времени t x и за это время его скорость возрастает от b до а градусов. Приращение скорости от b до а есть не что иное, как широта движения х. Пусть точно такая же широта движения «равномерно утрачивается» при равнозамедленном движении тела у за время t y(t x= t y). При этом предполагается, что движение у происходит с ускорением, равным (по абсолютной величине) ускорению x (точнее, Суайнсхед говорит не об ускорении, а о том, что а уменьшается и b возрастает при движении у и x равно быстро (equevelociter)). Последнее предположение реализуется в мысленном эксперименте в виде дополнительных требований, налагаемых на движение x и y: 1) x и y начинают двигаться одновременно;

2) «сколько одно (x) приобретает, столько другое (y) утрачивает». Если эксплицировать пункты, выполнение которых подразумевается краткой формулировкой второго требования, то они состоят в следующем. Пусть движение х, у начинается в момент времени t 0, a U обозначает произвольный момент времени их движения. В момент t ix будет иметь скорость b i(b i> b), а у — скорость a i(a i< a). Тогда в соответствии со вторым требованием b i—b = a—a i.

Если с = (a – b)/2, т. е. является средним градусом широты, то x и y достигнут с одновременно, так что x и y будут иметь одинаковую скорость с в момент t k(t k= (t i– t 0)/2), где t i— момент окончания движения х, у. Точнее, если обозначить через

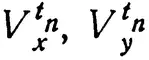
скорости x, y в момент времени t n, то

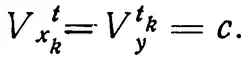
Отсюда

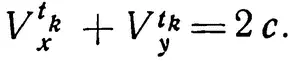
Но и для произвольного момента времени

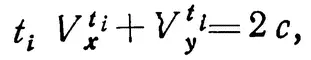
так как второе требование равносильно утверждению, что сумма скоростей x и y остается постоянной на протяжении всего движения.

Доказательством

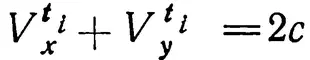
завершается, по существу, все доказательство теоремы у Суайнсхеда. Вывод о равенстве расстояний, проходимых при равноускоренном и равномерном движении со скоростью, равной среднему градусу широты первого, он считает столь очевидным, что предоставляет его сделать читателю. Действительно, из постоянства суммы скоростей V ti xи V ti y следует, что два равноускоренных движения, в результате которых проходится расстояние S = S x+ S y(S x, S y— расстояния, проходимые соответственно x и y), эквивалентны в отношении пройденного расстояния равномерному движению со скоростью V = 2c, продолжающемуся в течение того же времени. Поскольку S x= S y,то S xбудет пройдено за то же время при равномерном движении со скоростью с.