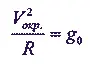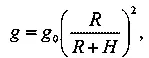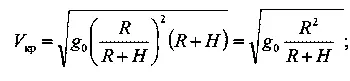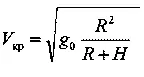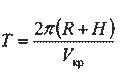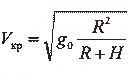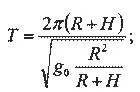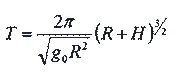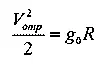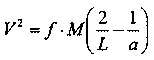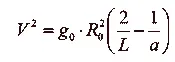Следовательно,
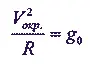
и
V окp= √ g 0 R ,
как и ранее.
Как изменяется круговая скорость с высотой орбиты спутника?
Очевидно; на высоте Н
V кp = √ g(R+H)
Но так как то
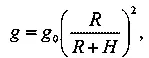
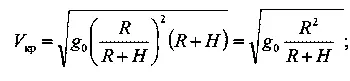
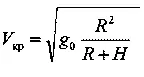
Это значит, что круговая скорость изменяется обратно пропорционально корню квадратному из расстояния до центра Земли.
| Высота Н в км |
Круговая скорость Vкр. в м/сек |
| 0 |
7 910 |
| 255 |
7 760 |
| 1 000 |
7 360 |
| 1 670 |
7 040 |
| 35 800 |
3 080 |
| 384 000 (орбита Луны) |
1 010 |
Б. Период обращения спутника
Время, за которое спутник совершит один полный оборот вокруг Земли, равно, очевидно, длине пути за оборот, деленной на круговую скорость:
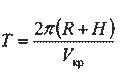
( Т — так называемый сидерический, или звездный, период обращения).
Но вследствие чего
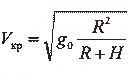
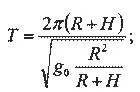
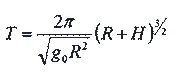
Подстановка значений R и g 0 дает следующую довольно точную для приближенных расчетов формулу:
T ≈ 0,01 ( R+H ) 3/2
| Высота Н в км |
Период обращения спутника Т в сек |
| 0 |
5 070 (1,4 часа) |
| 255 |
5 400 (1,5 часа) |
| 1 000 |
6 340 (1,76 часа) |
| 1 670 |
7 200 (2 часа) |
| 35 800 |
86 400 (24 часа) |
| 384 000 |
2,36·10 6 (27,3 суток) |
III. СКОРОСТЬ ОТРЫВА (ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ)
Скорость отрыва (или параболическая скорость) есть та скорость, которая должна быть сообщена телу у поверхности Земли, чтобы полностью преодолеть поле земного тяготения — удалить тело в бесконечность.
Величина скорости отрыва V отр. определяется тем, что кинетическая энергия тела должна в этом случае в точности равняться работе преодоления поля тяготения; с помощью высшей математики получаем:
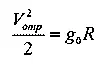
то есть работа полного преодоления поля земного тяготения равна работе поднятия тела при постоянном ускорении силы тяжести, равном его значению у земной поверхности g 0, на высоту земного радиуса R .
Так как √g 0R есть круговая скорость, то скорость отрыва V отp. в 1,41 раза больше круговой скорости:
V отр. = √2 V кр = 1,41· V кр
| Высота Н в км |
Скорость отрыва У отр. в км/сек |
| 0 |
11,2 |
| 300 |
10,9 |
| 1 000 |
10,4 |
| 1 670 |
9,9 |
| 35 800 |
4,3 |
| 384 000 |
1,42 |
IV. ОБЩИЙ ЗАКОН ДВИЖЕНИЯ КОСМИЧЕСКОГО КОРАБЛЯ В ПОЛЕ ТЯГОТЕНИЯ ОДНОГО НЕБЕСНОГО ТЕЛА
Примеры движения по кругу или по параболе, о которых шла речь выше, являются лишь частными случаями движения тела в поле тяготения небесного тела большой массы. Как известно из небесной механики, в общем случае орбитой такого движения является одна из кривых второго порядка (так называемых конических сечений): круг, эллипс, парабола или гипербола. Общий закон этого движения дается следующей формулой (так называемое уравнение живых сил, упрощенное для случая космического корабля, то есть тела небольшой массы):
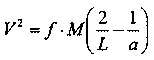
или где V — скорость движения тела массы пренебрежимо малой по сравнению с М ;
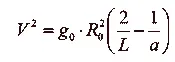
М — масса небесного тела;
f — гравитационная постоянная;
L — расстояние до центра тяжести небесного тела;
а — большая полуось орбиты;
g 0 — ускорение силы тяжести на поверхности небесного тела на расстоянии R 0 от его центра.
Читать дальше