Джеймс Гордон - Конструкции, или почему не ломаются вещи

Помнится, одно из книжных обозрений Дороти Паркер начиналось словами: "Эта книга рассказала мне о принципах бухгалтерского учета больше, чем мне хотелось бы знать" . Осмелюсь предположить, что поведение материалов и конструкций при сдвиге многие из нас склонны оставить специалистам. Кажется, что с растяжением и сжатием можно еще справиться, но относительно сдвига уверенности такой нет. Вдобавок к этому, если в учебниках по сопротивлению материалов говорится о сдвиге, то непременно в связи с какими-нибудь коленчатыми валами или балками особенно хитрых типов. После этих учебников, несмотря на их несомненную пользу, предмет нередко теряет всякую привлекательность и вдобавок при этом как-то ускользает от внимания тот простой факт, что напряжения сдвига и деформации сдвига возникают не только в балках и коленчатых валах, а практически во всех предметах, с которыми нам приходится иметь дело, и иногда это приводит к неожиданным последствиям. Именно из-за них дают течь суда, шатаются столы, в неожиданных местах вытягивается одежда. Если бы не напряжения сдвига, жить было бы легче и приятней не только инженерам, но и биологам, хирургам, плотникам-любителям и даже тем, кто выпускает болтающиеся чехлы для мебели.

Если растяжение - это когда тянут, сжатие - когда сдавливают, то сдвиг - это когда происходит взаимное проскальзывание. Другими словами, напряжение сдвига служит мерой тенденции к скольжению одной части твердого тела относительно другой. (Обратите внимание на скольжение карт в брошенной на стол колоде или ковра, когда его выдергивают у вас из-под ног.) Почти всегда сдвиг возникает и при скручивании, например в лодыжке, рулевой колонке или любой другой детали механизма. В условиях сдвига или кручения материалы обычно ведут себя довольно просто. Но прежде чем перейти к обсуждению особенностей этого поведения, нам необходимо договориться о терминологии. Поэтому мы начнем с нескольких определений.

Упругие свойства вещества при сдвиге очень похожи на его свойства при сжатии и растяжении, а такие понятия, как напряжение сдвига и деформация сдвига, аналогичны и не сложнее соответствующих понятий в случае растяжения.

Напряжение сдвига, или касательное напряжение, - τ. Как мы уже говорили, касательное напряжение служит мерой тенденции одной части твердого тела скользить относительно другой его части, как это схематически показано на рис. 118, а . Следовательно, если на поперечное сечение материала, имеющее площадь А , действует сдвигающая сила Р , то напряжение сдвига в некоторой точке материала будет [88] Это среднее значение касательного напряжения. - Прим. ред. : касательное напряжение = (перерезывающая сила / площадь ) = Р/ А = τ .

Касательное напряжение τимеет ту же размерность, что и растягивающее напряжение, например МН/м 2(кгс/мм 2).

Деформация сдвига - γ. Все твердые тела при действии напряжения сдвига деформируются аналогично тому, как это происходит и при растяжении. Однако в этом случае деформация представляет собой искажение углов и измеряется поэтому, как все углы, в градусах или радианах, чаще в радианах (рис. 118, б ). Радиан, конечно, не имеет размерности, будучи просто числом или отношением двух длин. Мы будем обозначать деформацию сдвига буквой γ: подобно относительной деформации растяжения, обозначаемой ε , γ- безразмерное число.

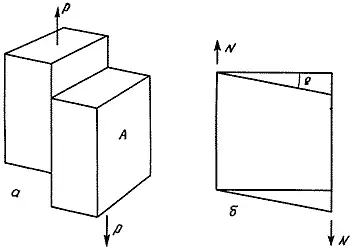
Рис. 118. Напряжение сдвига, или касательное напряжение, и деформация сдвига.

а - касательное напряжение = (перерезывающая сила / площадь) = Р/ А= τ .

б - деформация сдвига - это угол γ, на который искажается прямой угол в результате действия касательного напряжения τ.

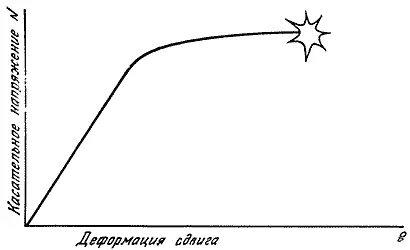
Рис. 119. Кривая деформирования при сдвиге похожа на соответствующую зависимость при растяжении.

Тангенс угла наклона прямолинейной части равен модулю сдвига: G = τ/ γ.

Для таких твердых тел, как металл, бетон или кость, упругая деформация сдвига обычно меньше 1° (1/57 радиана). При больших деформациях материалы этого типа либо разрушаются, либо испытывают необратимые пластические деформации - текут подобно сливочному маслу.