Сет Ллойд - Програмуючи Всесвіт. Космос – квантовий комп’ютер

Інакше кажучи, десять бітів відповідають трьом цифрам на позиціях «одиниці», «десятки» та «сотні», як ми традиційно рахуємо. Визначення кількості інформації – це просто лічба. Лічба бітами простіша, хоча менш відома, ніж лічба цифрами. Лічба цифрами від 0 до 9 проста: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. У цьому місці у вас, щоправда, цифри закінчуються, тож наступне число пишеться як 1, за яким іде 0, тобто 10. Число 10 має 1 у розряді десятків та 0 у розряді одиниць. Наступне число, 11, має 1 у розряді десятків і 1 у розряді одиниць. Ви можете продовжувати рахувати в цьому напрямку до 99. Наступним є число 100, що має 1 у розряді сотень, 0 у розряді десятків та 0 у розряді одиниць. (Тепер зрозуміло, чому так непросто засвоїти цей спосіб лічби вперше, коли вам років п’ять.)

Лічба бітами аналогічна. Починайте лічити: 0 = нуль, 1 = один. Поки що все йшло добре, але тепер у нас закінчилися біти. Наступною комбінацією бітів є 10, що дорівнює двом: тобто 1 у розряді «двійок» та 0 у розряді «одиниць». (Подання «двох» як «10» є особливістю двійкової арифметики, що завдає користувачеві-початківцю найбільше клопоту, як-от: «Існує 10 типів людей: ті, хто знає, що таке двійковий код, і ті, кому це невідомо».) Наступна комбінація – це 11, що дорівнює трьом: 1 у розряді двійок та 1 у розряді одиниць. Тепер у нас закінчилися двобітові числа.

Наступна комбінація – це 100, що дорівнює чотирьом: 1 у розряді четвірок, 0 у розряді двійок та 0 у розряді одиниць. Потім іде 101, що дорівнює п’яти (1 у розряді четвірок плюс 1 у розряді одиниць), 110 = шість, 111 = сім. Вісім представлене чотирма бітами: 1000, де одиниця в розряді вісімок, та 0 у розрядах четвірок, двійок та одиниць. Оскільки в них два біти замість десяти, двійкові числа подовжуються швидше, ніж звичайні.

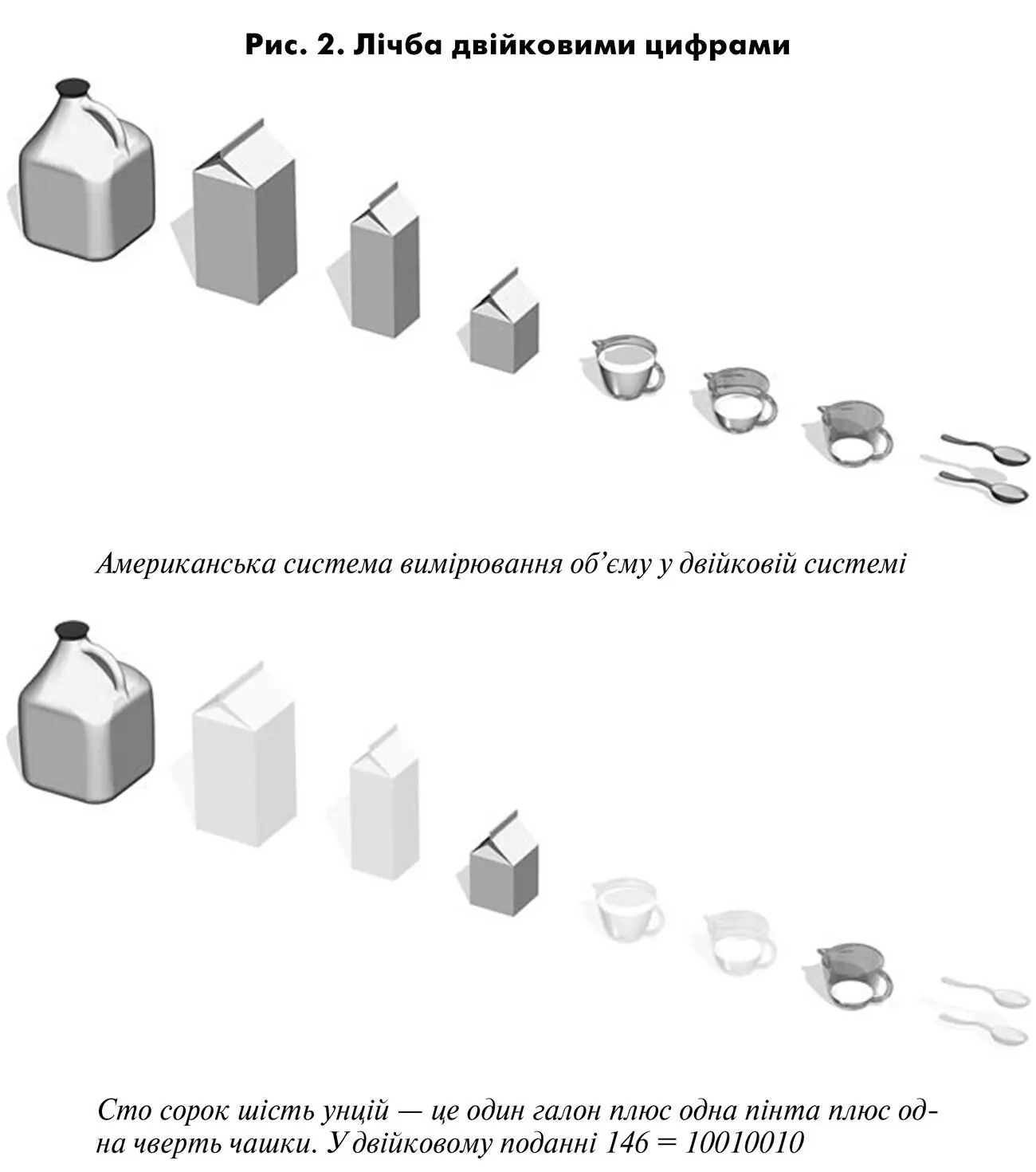
Як числа, кратні десятьом (десятки, сотні, тисячі, мільйони), важливі у звичайному, десятковому способі лічби, – так числа, кратні двом, важливі для лічби бітами: 1 = один = 2 0, 10 = два = 2 1, 100 = чотири = 2 2, 1000 = вісім = 2 3, 10000 = шістнадцять = 2 4, 100000 = тридцять два = 2 5, 1000000 = шістдесят чотири = 2 6, 10000000 = сто двадцять вісім = 2 7. Ці числа мають бути знайомі кулінарам. Англійська система мір та ваг – це двійкова система: вісім унцій у чашці, шістнадцять – у пінті (американській, бо британська пінта дорівнює двадцятьом унціям, а тройська – дванадцятьом), тридцять дві – у кварті, шістдесят чотири – у половині галона, сто двадцять вісім – у галоні загалом. Двійкове подання числа не складніше, ніж вимірювання у квартах, пінтах та унціях. Сто сорок шість унцій, наприклад, – це один галон плюс одна пінта плюс одна чверть чашки: 128+16+2 = 146. Написане двійковим способом 146 – це 10010010: одиниця в розряді «галонів», одиниця в розряді «пінт», одиниця в розряді «чвертей чашок», нулі в інших місцях. Щоб перевести число в двійкову систему, досить просто виміряти його чайними ложечками.

Лічба двійковим способом настільки ж проста (хоч і не для тих із нас, для кого це новина), як і двійкова арифметика. Уся двійкова таблиця додавання складається з: 0+0 = 0, 0+1 = 1, 1+1 = 10. Двійкове множення навіть простіше: 0 × 0 = 0, 0 × 1 = 0, 1 × 1 = 1. Двійкова система красива.

Двійкова система також застосовується на практиці. Компактність двійкового подання полегшує конструювання простих електронних схем для двійкових операцій. Ці схеми, своєю чергою, є основою цифрових комп’ютерів. Ми не в змозі визначити інформацію, але можемо використовувати її.

– А якщо є незліченне число варіантів? – спитав один студент. – Наприклад, існує незліченна кількість реальних чисел між 0 і 1.

– Якщо у вас є незлічена кількість варіантів, то у вас є незліченна кількість інформації, – відповів я.

Візьмімо двійкове число: 1001001 0110110 0100000 1110100 1101000 1100101 0100000 1100010 1100101 1100111 1101001 1101110 1101110 1101001 1101110 1101111, наприклад. За звичайною схемою кодування, відомою як ASCII 3 3 American Standard Code for Information Interchange – Американський стандартний код обміну інформацією. ( Прим. перекл. ) , кожній літері або машинописному символові відповідає семибітове кодове слово.

Це число, інтерпретоване в ASCII , відповідає символам I = 1001001, n = 1101110, (пробіл) = 0100000, t = 1110100, h = 1101000, e = 1100101, (пробіл) = 0100000, b = 1100010, e = 1100101, g = 1100111, i = 1101001, n = 1101110, n = 1101110, i = 1101001, n = 1101110, g = 1100111 – і виходить « In the beginning », тобто початок тексту: «Спочатку було слово…» Додаючи більше бітів, ви можете створити число, що відповідає всьому текстові Євангелія від Йоана. Додаючи ще більше, ви можете створити число всієї Біблії, потім – Корану, відтак – Сутри Лотоса, а далі – всіх книжок Бібліотеки Конгресу і так далі. Безмежна кількість варіантів відповідає безмежній кількості чисел, або бітів, іншими словами, безмежній кількості інформації.