Петр Силин - Некоторые аспекты оценки эффективности функционирования систем. Вторая редакция, исправленная и дополненная

Рисунок 6.2. иллюстрирует ситуацию, при которой вектор смещения {a} умозрительно перенесен в начало координат с сохранением длины и направления вектора (параллельный перенос). При таком переносе сохраняются и величины проекций вектора смещения на координатные оси, которые, будучи исчислены относительно начала системы координат, являются собственно координатами вектора смещения. Результатом сложения вектора {OA} и вектора смещения {a} по правилу параллелограмма дает все тот же вектор {OB} . Этот факт позволяет утверждать, что координаты вектора смещения, расположенного там, где ему полагается быть, и координаты вектора смещения, перенесенного в начало координат тождественны друг другу. Таким образом, координаты вектора смещения {a} , полученные в выражении (5), тождественны истинным координатам.

Заметим, что для нормализованных параметров этот вывод достигается, в общем-то, автоматически.

1.3.1.2. Множественные воздействия

При наличии нескольких источников воздействия на объект последний будет совершать движение в пространстве состояний, которое (движение) должно включать в себя ту или иную реализацию всех воздействий.

Рассмотрим два полярных случая:

– на рисунке 7.1 на объект, изначально находящийся в состоянии А , оказываются последовательные воздействия, т.е. каждое следующее воздействие инициируется после реализации смещения от предыдущего воздействия,

– на рисунке 7.2 на объект, находящийся в состоянии А оказывается несколько воздействий одновременно (для наглядности величина и количество воздействий совпадает с предыдущим вариантом).

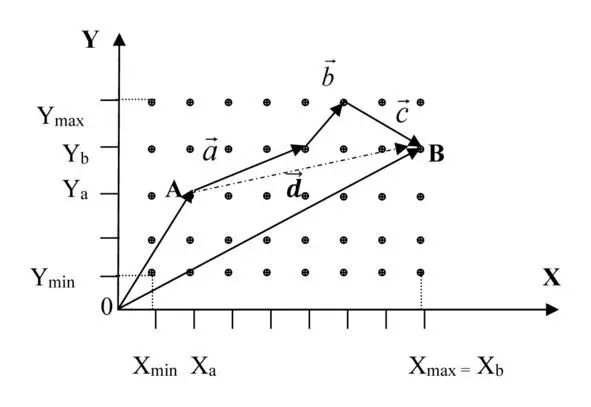
Рисунок 7.1 Вектор смещения, образующийся в результате ряда последовательных воздействий

Как видно из рисунка 7.1 на объект, находящийся в состоянии А , последовательно оказываются воздействия, приводящие к появлению векторов смещения {a} , {b} и {c} соответственно. В результате такого движения в пространстве состояний объект переходит в состояние В , вектор {OB} является результатом сложения векторов по правилу треугольников исходного вектора {OA} и совокупного вектора смещения {d} = {a} + {b} + {c} .

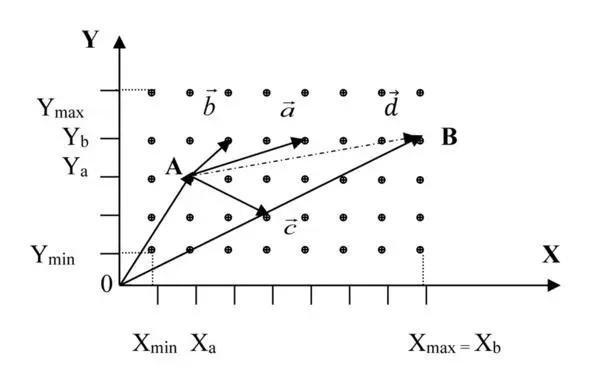
Рисунок 7.2 Вектор смещения, образующийся в результате одновременных воздействий

На рисунке 7.2 на объект оказывается сразу несколько воздействий, каждое из которых вызывает соответствующее смещение {a} , {b} и {c} соответственно. Можно убедиться, что если сложить векторы смещения по правилу параллелограмма, а потом результирующий вектор смещения {d} сложить с вектором исходного состояния {OA} либо по правилу треугольника, либо, предварительно параллельно сместив его в центр координат, сложить по правилу параллелограмма, мы получим вектор конечного состояния {OB} ,который, при совпадении частных векторов смещения {a} , {b} и {c} в обоих случаях воздействия, тождественен вектору {OB} , полученного при последовательны воздействиях, см. рисунок 7.1.

Полученные результаты позволяют сделать тот вывод, что при движении объекта в пространстве состояний в результате множественного воздействия характер воздействия (параллельный, последовательный или смешанный) на объект не имеет значения для образования результирующего вектора смещения.

1.3.2. Управляющие воздействия

Управляющие воздействия, как и любые другие воздействия, вызывают смещение объекта в пространстве состояний на ту или иную величину, в зависимости от величины воздействия.

Единственным отличием управляющего воздействия от любого другого является то, что управляющее воздействие всегда, независимо от того является ли оно внешним или внутренним, целенаправленно (правда не всегда удается эту цель достичь, да и система управления не всегда корректно определяет целевое состояние и/или вырабатывает управляющее воздействие).