ПИЛ ВИНО | ОН И ВЛИП.
Оборотни – штучный товар, их придумано гораздо меньше, чем палиндромов, а значит в этом направлении огромный простор для творческих поисков [?]
Несколько слов о симметрии математических объектов. Среди цифр двумя осями симметрии и центром симметрии обладают 0 и 8 (с оговоркой, что восьмерка имеет одинаковые по размерам верхний и нижний элементы), а если в качестве единицы брать римское изображение I, то она тоже обладает тремя видами симметрии. Аналогичной симметрией обладают знаки четырех основных математических действий +, -, ∙, : . Знак интеграла симметричен относительно центра. Цифра 3 обладает горизонтальной симметрией (с той же оговоркой). 9 – это горизонтальный оборотень, горизонтальное зеркало превращает ее в цифру 6, тот же эффект дает поворот цифры 9 относительно центра на 180 0. Поэтому, чтобы увеличить числа 6 или 66, или 666 в полтора раза, их нужно просто повернуть. В прошлом веке был год, который выражается числом, не изменяющимся при повороте листа с его записью – I96I.
Число 7 в вертикальном зеркале просто поворачивается в другую сторону, но если его записать как разность 8 – I, то зеркальная запись I – 8 означает -7. В этом примере проявляется аналогия зеркального отражения и умножения на -1. Некоторые дроби при отражении в горизонтальном зеркале дают обратные числа:
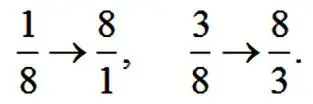
Римские цифры применяются сейчас редко, но симметрии в них больше, чем в арабских цифрах. Только L=50 не обладает никакой симметрией, все остальные, так или иначе, симметричны. Посмотрите на их ряд и составьте свое мнение о видах симметрии этих цифр и чисел: I, II, III, IV, V, VI, VII, VIII, IX, X, L, C, D, M.
[?-5]
С помощью зеркала и римских чисел можно построить парадоксальную таблицу умножения, в которой дважды четыре – девять, дважды шесть – одиннадцать, дважды семь – двенадцать, дважды восемь – тринадцать. Как это может получаться?
Перевертыши – Антифразы – Антонимы
Словесную игру в перевертыши можно было увидеть в телевизионной передаче «Великолепная семерка». Была когда-то такая развивающая передача. О том, что теперь показывают нам «кривые зеркала» лучше не думать. Некоторое время игра в перевертыши встречалась в газетах «Поле чудес» и «Русский кроссворд», специализирующихся на головоломках. В Интернете можно встретить и другое название перевертышей – антифразы.
Прежде чем разбираться в этом понятии, нужно вспомнить известное из школы значение слова антоним. Слово антоним происходит от греческих anti – против и onyma – имя. Антонимами называют слова с противоположным значением: горячий – холодный, горе – радость, враг – друг, мало – много, всегда – никогда, далеко – близко, до – после . Антонимы – это слова, которые могут обозначать степень признака ( тихий – громкий ), противоположно направленные действия ( поднимать – опускать ), точки пространства и времени, расположенные как бы на разных полюсах ( верх – низ, поздно – рано ).
Рассмотрим разновидности антонимов:
1. В простейшем случае к слову можно подобрать антоним, добавив в качестве предлога частицу отрицания ( люди – нелюди, приязнь – неприязнь ). Такие пары слов не представляют особого интереса, предложения с использованием таких пар звучат сухо.
2. Следующий вариант мало отличается от предыдущего, разница лишь в том, что предлог замещается, а не добавляется ( бессилие – всесилие, симпатия – антипатия, неизвестность – известность ).
3. Наиболее интересный случай – разнокоренные слова ( легкомысленность – серьезность, запад – восток ).
4. В качестве антонимов можно использовать и собственные имена существительные, по сути не являющиеся антонимами (Монтекки – Капулетти), если в контексте заостряется внимание на противоположностях.
Слова, которые обозначают конкретные предметы, обычно не имеют антонимов ( шкаф, штора, варенье ).
Математика богата антонимами – это знаки, числа, операции:
плюс – минус
положительное – отрицательное
сложение – вычитание
умножение – деление
больше – меньше
делитель – кратное
прямая – кривая
параллельно – перпендикулярно
простое число – составное число
дифференцирование – интегрирование
возведение в степень – извлечение корня.
Читать дальше
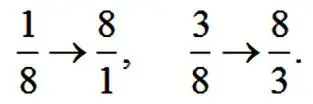

![Владимир Трошин - Княжич [СИ]](/books/404433/vladimir-troshin-knyazhich-si-thumb.webp)









