Владимир Петров - Инновации. Бизнес. ТРИЗ. Теория решения изобретательских задач

Сравнивая реальное решение с ИКР, определяем противоречие. Таким образом, ИКР – инструмент, необходимый для выявления противоречия, нахождения задач и для оценки качества решения. Следовательно, ИКР служит своего рода «путеводной звездой» при решении бизнес- задач.

Выявление противоречия свойств при решении задач требует определенной направленности поиска, что возможно только при знании ответа. В реальной задаче ответ, безусловно, не известен.

Направленность в решении может быть достигнута ориентировкой на законы и закономерности развития системи, прежде всего, на закономерность увеличения степени идеальности системы .

При решении нестандартных задач эта закономерность проявляется ориентацией на идеальный результат – ИКР.

Рассмотрев основные понятия: идеальный конечный результат (ИКР), поверхностное противоречие (ПП), противоречие требований (ПТ) и противоречие свойств (ПС) – мы легко себе можем представить этапы точной формулировки задачи.

Окончательно основную линию решения нестандартных задач можно представить в следующем виде:

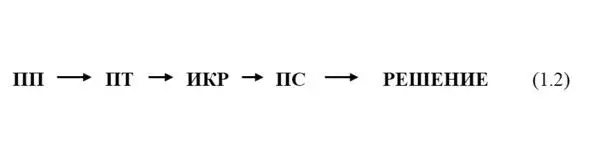
Задача точно сформулирована, когда выявлены ПП, ПТ, ИКР, ПС, согласно приведенной цепочке (1.2).

Для формулировки всех ее звеньев прежде всего выявляют, чем не устраивает «задачедателя» данная система ( ПП), и что в ней плохого ( нежелательный эффект ).

Далее определяют требования, которые необходимо предъявить к системе. Так определяется ПТ.

Затем систему представляют таким образом, что в ней отсутствует нежелательный эффект , но сохраняются имеющиеся положительные качества . Результатом такого представления системы является формулировка ИКР.

После сравнения противоречия требований (ПТ) с ИКР выявляют помехи к достижению идеального результата, ищутся причины возникновения помех и определяют противоречивые свойства (ПС) , предъявляемые к определенной части системы (к оперативной зоне ), не удовлетворяющие требованиям ИКР. Таким образом, формулируется ПС, которое и представляет собой точную формулировку задачи. Разрешая противоречивые свойства, указанные в ПС, получают решениебез недостатков.

Г. С. Альтшуллер писал: «Простоту ответа иногда принимают за простоту процесса решения. Между тем, чем проще ответ (если речь идет о задачах высших уровней), тем труднее его получить» 2 2 Альтшуллер Г. С. Творчество как точная наука . Теория решения изобретательских задач. – М.: Сов. радио, 1979. – 184 с. – Кибернетика (С. 51) .

Иногда для разрешения противоречия свойств (ПС), т. е. разделения выявленных противоречивых свойств, достаточно воспользоваться приемами, указанными выше, (в пространстве, во времени, в структуре и по условию), а иногда нужно продолжить анализ противоречий. Главное, чтобы решение удовлетворяло требованиям ИКР.

До разделения противоречивых свойств ПС желательно проделать анализ на возможность изменения требований ПТ и свойств ПС.Назовем это « Анализ ПТ и ПС».

Такой анализ проводится следующим способом:

1. Желательно выяснить какое из требований ПТ более важное и его нежелательно или невозможно менять, а какое может быть изменено.

1.1. В соответствии с этим выбирают свойство ПС, которое останется неизменным. Затем определяют, как разделить противоречивые свойства ПС, чтобы удовлетворить ИКР. Пример – задача 2.2 (ИТ безопасность)

1.2. Если должно обязательно происходить в одно и тоже время, то ПС может разрешиться, например, в пространстве или в структуре. Пример – задача 2.4 (инвестирование).

1.3. Если должно обязательно происходить в одном и том же пространстве, то ПС может разрешиться, например, во времени. Пример – задача 2.3 (поставка пшеницы).

1.4. Создать условия, при которых важное требование ПТ будет обязательно выполнено. Пример – задача 2.5 (такси).

2. В случае одинаковой важности обоих требований ПТ стоит проверить, не включает ли в себя хотя бы одно из них несколько признаков.

2.1. Нельзя ли это требование разделить на составные части и провести анализ обязательности каждой из частей. Возможно, какая-то из частей может быть необязательной. Тогда, вероятно, за счет изменения этой части можно получить решение, используя все имеющиеся способы разрешения противоречий.