Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Математика, стоящая за этой проблемой, сложна, но оказывается, что следует оценить и отвергнуть примерно первые 37 % ресторанов (округленные до трех, если их всего 10), прежде чем выбрать следующий, который лучше всех предыдущих. Точнее, нужно отвергнуть 1/e долю всех доступных вариантов, где e – математическое обозначение числа Эйлера [158]. Число Эйлера составляет приблизительно 2,718, таким образом, 1/e – примерно 0,368 или, в процентном соотношении, 37 %. Рис. 22 иллюстрирует, как меняется вероятность выбора лучшего из 100 ресторанов по мере того, как вы варьируете количество ресторанов, которые отвергаете сразу. Если вы поспешите с решением, оно, по сути, сведется к слепому гаданию, поэтому неудивительно, что при слишком раннем выборе вероятность наткнуться на лучший ресторан низка. Аналогично, если вы выбираете слишком долго, то, скорее всего, вы уже пропустили лучший вариант. Вероятность наилучшего выбора максимальна, когда вы отклоняете первые 37 вариантов.

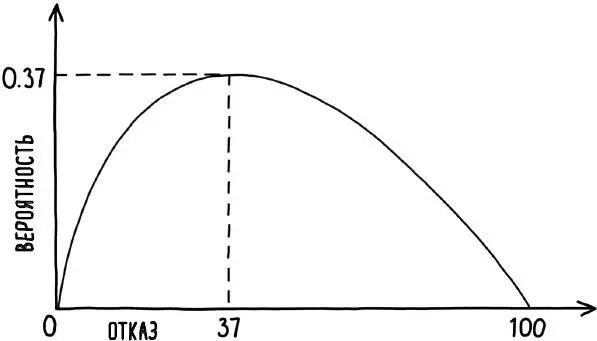
Рис. 22. Вероятность выбора наилучшего варианта максимальна, когда мы оцениваем и отклоняем 37 % вариантов, прежде чем принять следующий, который оценим выше, чем все, что видели прежде. В этом сценарии вероятность выбора лучшего ресторана составляет 0,37, или 37%

Но что, если лучший ресторан был в первых 37 %? В таком случае, вам не повезло. Правило 37 % работает не каждый раз – оно вероятностное. Вообще алгоритм гарантированно работает только в 37 % случаев. Это лучшее, что вы можете сделать в данных обстоятельствах, но это выгоднее, чем 10-процентный шанс на успех, если бы вы выбирали один из 10 ресторанов наугад, и намного выгоднее, чем 1-процентный, если бы вам пришлось выбирать между 100 ресторанами. Чем выше относительная вероятность успеха, тем шире ваш выбор.

Стратегия оптимальной остановки работает не только для ресторанов. На самом деле изначально математики окрестили ее «проблемой найма» [159]. Если вы должны по очереди провести собеседование с конечным количеством кандидатов на должность, в конце каждого собеседования сообщив претенденту, получил ли он работу, используйте правило 37 %. Проведите собеседование с 37 % кандидатов и используйте их в качестве ориентира. Возьмите после этого первого кандидата, который окажется лучше всех тех, кого вы видели до него, и откажите остальным.

Когда я подхожу к кассам в моем местном супермаркете, я прохожу мимо первых 37 % (4 из 11), отмечая длину очереди в каждую из них, а затем встаю в первую же очередь, которая короче, чем все остальные, которые я видел. Если я вместе с группой друзей пытаюсь сесть в забитый пассажирами последний поезд после затянувшейся гулянки – да еще так, чтобы мы сели все вместе, мы используем правило 37 %. Мы пробегаем мимо первых трех вагонов состава, который состоит из восьми вагонов, запоминая, сколько в них народу, а затем садимся в первый же вагон, в котором больше свободных мест, чем в любом из первых трех.

Некоторые из этих сценариев несколько надуманны – хотя и навеяны реальным опытом. Но их можно сделать более прагматичными. Что произойдет, если в половине ресторанов, которые вы проверите, не будет свободных мест? В таком случае логично будет сократить время на предварительный отсев ресторанов. Вместо того чтобы проверять первые 37 %, проверьте только первые 25 %, прежде чем выбирать тот, что будет лучше всех остальных, которые вы уже видели.

Или если вы решите, что у вас достаточно времени, чтобы рискнуть – и вернуться к одному из тех вагонов поезда, которые пропустили, но вероятность, что он за это время заполнится, составляет 50 %? Возвращаясь, вы расширяете свои возможности и можете позволить себе искать немного дольше – отказаться от 61 % вагонов впереди перед тем, как выбрать следующий более пустой вагон. Не забывайте, однако, что вам все-таки нужно сесть в поезд прежде, чем он отойдет.

Существуют алгоритмы оптимальной остановки, которые могут подсказать, когда продать свой дом или на каком расстоянии от кинотеатра стоит искать парковку, чтобы шансы найти свободное место были максимальными, а пеший путь до кинотеатра – минимальным. Подвох в том, что чем реалистичнее ситуация, тем сложнее становятся математические выкладки, и простые процентные правила уже не действуют.

Существуют даже алгоритмы оптимальной остановки, которые подскажут, сколько кавалеров (или пассий) вам нужно перебрать, прежде чем задумываться о браке. Сначала нужно решить, сколько увлечений вы захотите пережить к тому времени, когда пожелаете остепениться. Допустим, вы остановитесь на одном романе в год с 18 по 35 лет, что составит в общей сложности 17 потенциальных партнеров на выбор. Стратегия оптимальной остановки предполагает, что вы играете на этом поле около шести или семи лет (примерно 37 % от 17 лет), определяясь с выбором. После этого вы должны остаться с первым же человеком, который вам подойдет лучше всех тех, с кем вы встречались до того.