Мы назовем самую длинную его сторону (с, она всегда напротив прямого угла) гипотенузой. Ту сторону, что противостоит избранному нами углу (в данном случае А), мы назовем противоположным катетом, а примыкающую к углу сторону – прилегающим катетом. Случайным образом сумма углов любого треугольника дает 180 градусов, а поскольку мы знаем, что прямой угол равен 90, то для того, чтобы узнать значения других углов, нам необходимы сведения только об одном из них.
Вот полезная теорема, касающаяся прямоугольных треугольников:
a 2+ b 2= c 2
Ее называют «теоремой Пифагора» по имени чувака, откликавшегося на Пифагора в античной Греции около 500 до н. э., но даже он признавал, что не был первым, кому эта идея пришла в голову. Теорема эта независимым образом открывалась до него и после него в разных частях мира. Она говорит, что сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины гипотенузы, что позволяет нам вычислять все характеристики прямоугольного треугольника, имея неполные данные, и именно этим, как мы уже сказали, тригонометрия по большей части и занимается.
Если вы знаете углы прямоугольного треугольника, то вы можете описать его форму, поскольку есть только один способ, которым могут сочетаться конкретные углы, чтобы сформировать треугольник. И это значит, что противоположное утверждение также истинно: если вы знаете длины сторон прямоугольного треугольника, то вы знаете и углы.
Это позволяет нам выполнять некоторое количество полезных операций.
Отношение длины противоположного катета к длине гипотенузы мы назовем «функцией синуса», или sin для краткости. Отношение длины прилегающего катета к длине гипотенузы мы назовем «косинусом», или cos для краткости [247], а отношение длины противоположного катета к прилегающему поименуем «тангенсом» (он же tan).
Имея в распоряжении угол, мы можем определить для него значения синуса, косинуса и тангенса. С другой стороны, зная величины этих функций, мы можем понять, о каком угле идет речь. Мы будем отмечать обратные величины с помощью крохотной «–1», отсюда у нас появляются sin -1, cos -1, tan -1.
По мере того как вы будете исследовать тригонометрию, вы обнаружите доказательства того, что эти величины связаны с параметрами определенных кругов (нарисуйте круг вокруг вашего треугольника, и вы увидите связи между числом пи и синусом, косинусом и тангенсом), заметите определенные шаблоны в этих функциях (поместите их значения в таблицу, и вы обнаружите, как повторяются их значения) и даже связи тригонометрических функций между собой (как пример: тангенс угла равен синусу, поделенному на косинус этого угла). Все это сказано к тому, что если эта наука вас интересует, то тут масса материала для изучения, и многие посвятили целую жизнь куда менее значимым и благородным темам [248].
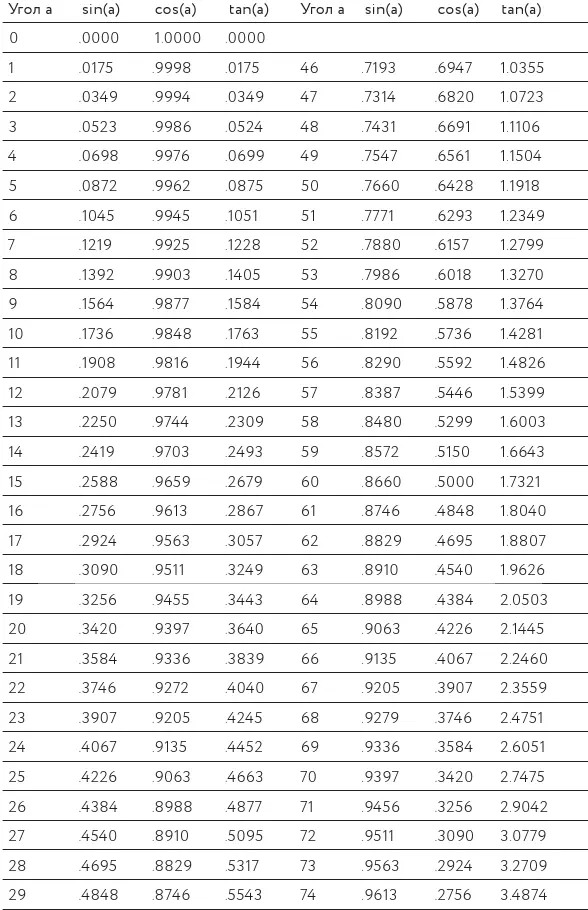
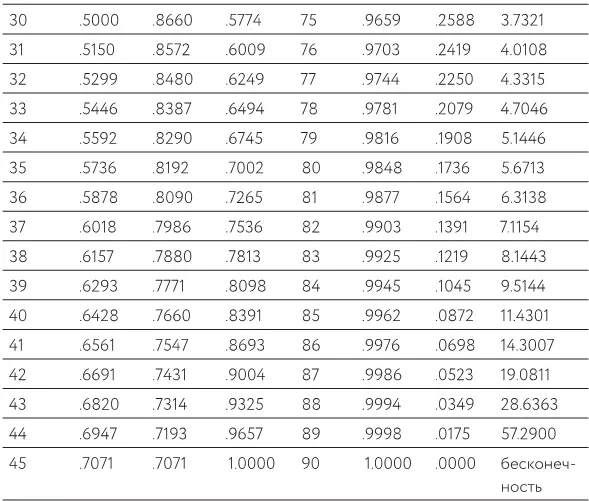
Фишка в том, что просто рассчитывать значения синуса, косинуса и тангенса достаточно трудно и сделать это нужно всего один раз. Так что, вместо того чтобы заставить вас делать это самостоятельно, ваши друзья из «Хронотикс Солюшн» взяли и включили в этот раздел полные тригонометрические таблицы (табл. 29).
Зная угол a, вы можете определить значения sin (a), cos (a) и tan (a).
А чтобы использовать обратные функции (sin -1, cos -1, tan -1), просто найдите угол, который соответствует имеющемуся у вас значению.
То, что находится ниже, потребуется вам для изучения тригонометрии, изобретения новых теорем и тригонометрических уравнений, а также для успешного завершения работы над солнечными часами из раздела 10.7.1.
Таблица 29.Вот вам числа, которые требуются, чтобы заставить треугольники работать
Приложение F
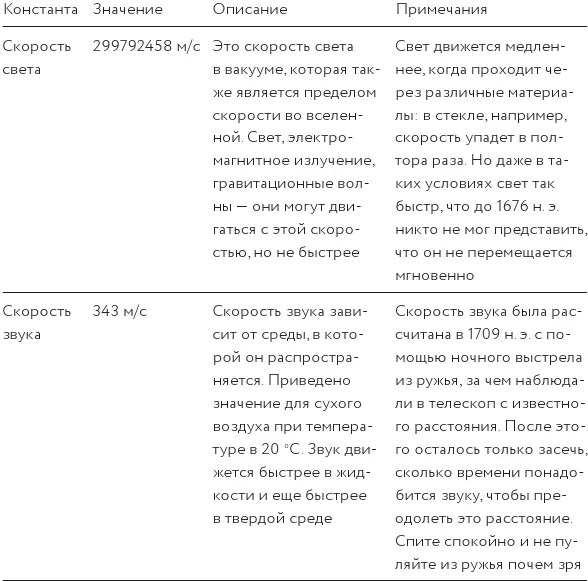
Некоторые универсальные константы, на обнаружение которых у человечества ушло немало времени и которые вы можете назвать собственным именем
Таблица 30.Вот числа, которые нужны вам, чтобы заставить работать саму реальность


 Читать дальше
Читать дальше
Конец ознакомительного отрывка
Купить книгу


















