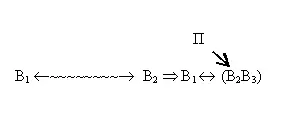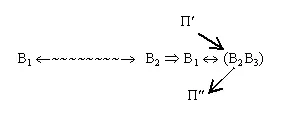Генрих Альтов - Творчество как точная наука. Теория решения изобретательских задач

В' - состояние вещества на входе;

В'' - состояние вещества на выходе;

В' - В'' - «переменное» вещество, находящееся то в состоянии В', то в состоянии В'' (например, под действием переменного поля);

- переменное поле.

В вепольных формулах вещества надо записывать в строчку, а поля сверху и снизу; это позволяет нагляднее отразить действие нескольких полей на одно и то же вещество.

На первых порах представление технических систем в виде веполей наталкивается на чисто психологические трудности. Нечто подобное наблюдается при освоении ребенком понятия «треугольник». Почему три яблока, лежащие в сумке, это не треугольник, а те же три яблока, расположенные на столе, образуют треугольник? Почему три точки дают треугольник и три дома тоже дают треугольник, хотя точки очень маленькие, а дома очень большие?.. Эти затруднения довольно быстро преодолеваются,

Кстати, об аналогии с геометрией. Треугольник - минимальная геометрическая фигура. Любую более сложную фигуру (квадрат, ромб, четырехугольник и т. д.) можно свести к сумме треугольников. Именно поэтому изучение свойств треугольника выделено в особую науку-тригонометрию. - система из трех элементов В1, В2 и П - играет в технике такую же фундаментальную роль, какую треугольник играет в геометрии. Зная несколько основных правил и имея таблицы тригонометрических функций, можно легко решать задачи, которые без этого потребовали бы кропотливых измерений и вычислений. Точно так же, зная правила построения и преобразования веполей, можно легко решать многие трудные изобретательские задачи.

Первое правило, с которым мы уже познакомились, состоит в том, что невепольные системы (один элемент - вещество или поле) и неполные вепольные системы (два элемента - поле и вещество, два вещества) необходимо - для повышения эффективности и управляемости - достраивать до полного веполя (три элемента - два вещества и поле).

Выше была приведена задача 3 о разделении щепы древесины и коры. В ней даны два вещества, и, следовательно, для достройки веполя необходимо ввести поле. Огромное поисковое пространство резко сужается; нужно рассмотреть всего несколько вариантов. В сущности, если отбросить поля сильных и слабых взаимодействий (в данной задаче они явно ведут к слишком сложным решениям), остаются два «законных» поля: электромагнитное и гравитационное. Учитывая ничтожную разницу в удельном весе щепок, следует сразу отбросить и гравитационное поле. Остается одно поле - электромагнитное. Поскольку магнитное поле не действует на кору и древесину, можно сразу ставить решающий эксперимент: как ведут себя щепки в электрическом поле? Оказывается, в электрическом поле частицы коры заряжаются отрицательно, а частицы древесины - положительно. Это позволяет построить сепаратор, обеспечивающий надежное разделение щепок.

Ну, а если бы щепки не электризовались? И в этом случае правило о постройке веполя сохраняет силу. Задача состоит в том, чтобы удалить один вид щепок. Следовательно, мы имеем право считать, что дано одно вещество, которое надо перемещать. Достроим веполь: добавим к этому веществу пару «вещество и поле». Например, до раздробления ствола и ветвей нанесем на кору ферромагнитные частицы, а затем - после дробления - используем для сепарации магнитное поле. Тут уже не требуются эксперименты: магнитное поле заведомо способно перемещать «омагниченную» кору.

Это решение можно изобразить так:

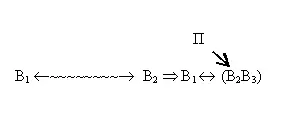
Дана смесь двух веществ, эти вещества сами не хотят разделяться. Решение состоит в достройке веполя, причем вместо В2 надо взять комплекс (В2 В3).

Возможность строить «комплексные» веполи намного расширяет область применения правила о достройке веполя.

Решение задачи 9 тоже можно рассматривать как построение комплексного веполя (в жидкость добавлен люминофор):

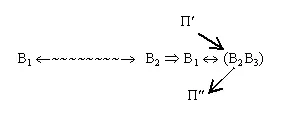
Здесь В1- холодильный агрегат; В2 - холодильная жидкость; В3 - люминофор; П- поле на входе (невидимое ультрафиолетовое излучение); П - поле на выходе (видимое излучение люминофора).

Правило достройки веполя непосредственно вытекает из самого определения понятия «веполь»: минимально полная техническая система заведомо эффективнее неполной системы, поэтому данные в задачах невепольные и неполные вепольные системы надо достраивать до полных веполей. Существуют и другие правила, относящиеся к построению и преобразованию вепольных систем. Использование этих правил лежит в основе вепольного анализа, составляющего один из важнейших разделов теории решения изобретательских задач. Приведем задачу.