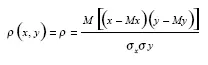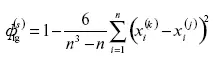ЛЕКЦИЯ № 13. Корреляционно–регрессионный анализ
1. Понятие и виды корреляционного анализа
К. Пирсон и Дж. Юл разработали корреляционный анализ, который по их мнению должен ответить на вопрос о том, как выбрать с учетом специфики и природы анализируемых переменных подходящий измеритель статистической связи (коэффициент корреляции, корреляционное отношение, и т.д.), решить задачу как оценить его числовые значения по уже имеющимся выборочным данным.
Корреляционный анализ поможет: найти методы проверки того, что полученное числовое значение анализируемого измерителя связи действительно свидетельствует о наличии статистической связи; определить структуру связей между исследуемыми k признаками х1, х2,…, хк, сопоставив каждой паре признаков ответ («связь есть» или «связи нет»).
Парный коэффициент корреляции – основной показатель взаимозависимости двух случайных величин, служит мерой линейной статистической зависимости между двумя величинами., он соответствует своему прямому назначению, когда статистическая связь между соответствующими признаками в генеральной совокупности линейна. То же самое относится к частным и множественным коэффициентам корреляции.
Парный коэффициент корреляции, характеризует тесноту связи между случайными величинами х и у, определяется по формуле:
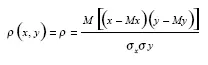
Если р = 0, то между величинами х и у линейная связь отсутствует и они называются некоррелированными.
Коэффициент корреляции, определяемый по вышеуказанной формуле, относится к генеральной совокупности.
Частный коэффициент корреляции характеризует степень линейной зависимости между двумя величинами, обладает всеми свойствами парного, т.е. изменяется в пределах от–1 до +1. Если частный коэффициент корреляции равен ±1, то связь между двумя величинами функциональная, а равенство его нулю свидетельствует о линейной независимости этих величин.
Множественный коэффициент корреляции, характеризует степень линейной зависимости между величиной х 1и остальными переменными (х 2, х 3), входящими в модель, изменяется в пределах от 0 до 1.
Ординальная (порядковая) переменная помогает упорядочивать статистически исследованные объекты по степени проявления в них анализируемого свойства.
Ранговая корреляция – статистическая связь между порядковыми переменными (измерение статистической связи между двумя или несколькими ранжировками одного и того же конечного множества объектов О 1О 2,…, О п.
Ранжировка – это расположение объектов в порядке убывания степени проявления в них k– го изучаемого свойства. В этом случае x (k)называют рангом i – го объекта по k – му признаку. Раж характеризует порядковое место, которое занимает объект О iв ряду п объектов.
К. Спирмен в 1904г предложил показатель, который служил для измерения степени тесноты связи между ранжировками
х 1 (k),x 2 (k),..,x n (k) и х 1 (i),x 2 (i),..,x n (i)
В последствии данный коэффициент был назван ранговым коэффициентом К. Спирмен:
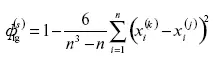
2. Методы регрессионного анализа
Термин «регрессия» ввел английский психолог и антрополог Ф.Гальтон.
Для точного описания уравнения регрессии необходимо знать закон распределения результативного показателя у. В статистической практике обычно приходится ограничиваться поиском подходящих аппроксимаций для неизвестной истинной функции регрессии Д(х), так как исследователь не располагает точным знанием условного закона распределения вероятностей анализируемого результатирующего показателя у при заданных значениях аргумента х.
Рассмотрим взаимоотношение между истинной f(х) = М(у/х). модельной регрессией у и оценкой у регрессии. Пусть результа–тив–ный показатель у связан с аргументом х соотношением:
у=2х 1,5 + ε i,
где E i – случайная величина, имеющая нормальный закон распределения, причем M ε= 0 и d ε – δ 2.
Истинная функция регрессии в этом случае имеет вид:
f(х) = М(у/х) = 2х 1 1,51,5+ε i
Для наилучшего восстановления по исходным статистическим данным условного значения результативного показателя f(х) и неизвестной функции регрессии /(х) = М(у/х) наиболее часто используют следующие критерии адекватности (функции потерь).
Читать дальше
Конец ознакомительного отрывка
Купить книгу