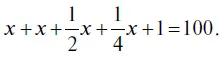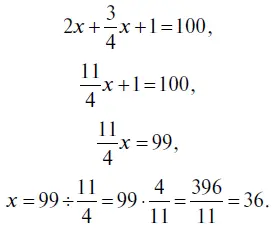Дмитрий Гусев - Удивительная логика

97. Собеседник просит вас задумать любое трехзначное число, а потом предлагает записать его цифры в обратном порядке, чтобы получилось еще одно трехзначное число. Например, 528–825, 439–934 и т. п. Далее он просит от большего числа отнять меньшее и сообщить ему последнюю цифру разности. После этого он называет разность. Как он это делает?

98. Семеро шли – семь рублей нашли. Если бы не семеро, а трое пошли, то много бы нашли?

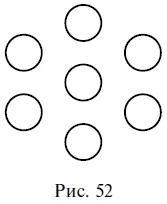
99.Разделите рисунок, состоящий из семи кружочков, тремя прямыми линиями на семь частей таким образом, чтобы в каждой части находился один кружочек (рис. 52).

100.Земной шар стянули обручем по экватору. Потом длину обруча увеличили на 10 метров. При этом между поверхностью Земного шара и обручем образовался небольшой зазор. Сможет ли человек пролезть в этот зазор? Длина земного экватора приблизительно равна 40 000 километрам.

1. Из первого мешка надо вытащить одну монету, из второго – две, из третьего – три, и т. д. (из десятого мешка – все 10 монет). Далее следует один раз взвесить все эти монеты вместе. Если бы среди них не было фальшивых монет, т. е. все они были бы весом по 10 граммов, то общий их вес составил бы 550 граммов. Но поскольку среди взвешиваемых монет есть фальшивые (по 11 граммов), то их общий вес будет больше 550 граммов. Причем, если он окажется 551 грамм, то фальшивые монеты находятся в первом мешке, ведь из него мы взяли одну монету, которая и дала один лишний грамм. Если общий вес будет 552 грамма, значит, фальшивые монеты находятся во втором мешке, ведь из него мы взяли две монеты. Если общий вес будет 553 грамма, значит, фальшивые монеты находятся в третьем мешке, и т. д. Таким образом с помощью только одного взвешивания можно точно установить, в каком мешке находятся фальшивые монеты.

2. Надо взять печенье из банки с надписью «Овсяное печенье» (можно из любой другой). Так как банка надписана неправильно, то это будет песочное печенье или шоколадное. Допустим, вы достали песочное. После этого надо поменять местами этикетки «Овсяное печенье» и «Песочное печенье». А поскольку по условию все этикетки перепутаны, то теперь в банке с надписью «Шоколадное печенье» находится овсяное, а в банке с надписью «Овсяное печенье» находится шоколадное, значит, надо поменять местами и эти две этикетки.

3. Из шкафа нужно достать только три носка. При этом возможно всего 4 варианта: все три носка белые; все три носка черные; два носка белые, один черный; два носка черные, один белый. В каждой из этих комбинаций имеется одна совпадающая пара – белая или черная.

4. Часы пробьют 12 часов за 66 секунд. Когда часы бьют 6 часов, то от первого удара до последнего проходит 5 интервалов. Интервал составляет 6 секунд (1/5 часть от 30). Когда часы бьют 12 часов, то от первого удара до последнего проходит 11 интервалов. Так как длина интервала равна 6 секундам, то, для того чтобы пробить 12 часов, часам требуется 66 секунд: 11 · 6 = 66.

5. Пруд будет покрыт листьями лилии наполовину на 99-й день. По условию число листьев каждый день удваивается, и если на 99-й день пруд покрыт листьями наполовину, то на следующий день и вторая половина пруда будет покрыта листьями лилии, т. е. полностью пруд покроется ими через 100 дней.

6. Путь, пройденный на пятый этаж (4 пролета) пассажирским лифтом, вдвое больше пути, пройденного на третий этаж (2 пролета) грузовым. Поскольку пассажирский лифт идет в 2 раза быстрее, чем грузовой, то они пройдут свои пути одновременно.

7. Для решения этой задачи надо составить уравнение. Количество гусей в стае – это х . «Вот если бы нас было столько, сколько сейчас (т. е. х ), – сказали гуси, – да еще столько (т. е. х ), да еще пол-столько (т. е. 1/2 х ), да еще четверть-столько (т. е. 1/4 х ), да еще ты (т. е. 1 гусь), вот тогда нас было бы 100 гусей». Получается следующее уравнение:

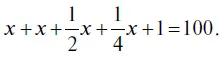
Произведем сложение в левой части равенства:

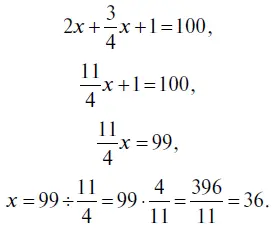
Итак, в стае было 36 гусей.

8. Ошибка заключается в возведении каждой части равенства —2 = 2 в квадрат. Создается видимость, что над каждой частью равенства совершается одна и та же операция (возведение в квадрат), на самом же деле над каждой частью равенства совершаются различные операции, ведь левую часть мы умножаем на —2, а правую умножаем на 2.