36.С помощью единственной черточки один из знаков плюс превратится в цифру четыре, в результате чего получается равенство:
545 + 5 = 550.
Вот эта черточка: → 5'+ 5 + 5 = 550.
37.В этом рассуждении в одних и тех же словах смешиваются различные математические операции: деление на два и умножение на два. На этом смешении и основан подвох в виде внешне правильного доказательства ложной мысли.
38. См. рис. 58.
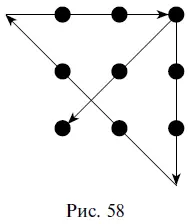
39.Номер для квартиры.
40. Нельзя, так как через 72 часа, т. е. через трое суток, будет опять 12 часов ночи, а солнце ночью не светит (если, конечно, дело не происходит за Полярным кругом в полярный день).
41. У хозяйки 25 рублей, у мальчика 2 рубля. Всего 27 рублей, значит, те 2 рубля, которые получил мальчик, входят в 27 рублей. А в условии задачи к 27 рублям прибавлено 2 рубля, которые у мальчика, и поэтому получается 29 рублей. Надо к 27 рублям не прибавлять 2 рубля, а отнимать.
42.1 л равен 1 дм 3. Следовательно, в бассейн налили 1 000 000 дм 3воды, или 1000 м 3воды (так как 1 м равен 10 дм). Зная площадь бассейна (1 га = 10 000 м 2) и объем налитой в него воды, легко вычислить его глубину:
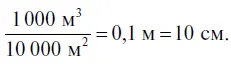
В бассейне глубиной 10 сантиметров плавать невозможно.
43. Для сравнения указанных величин надо привести квадратный корень и кубический к корню одной степени. Это может быть корень шестой степени. Соответственно изменятся и подкоренные выражения. Получится 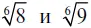 . Корень шестой степени из девяти немного больше такого же корня из восьми, следовательно,
. Корень шестой степени из девяти немного больше такого же корня из восьми, следовательно, 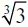 больше, чем
больше, чем 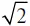 .
.
44. Обозначим стоимость линейки как х . Тогда у одного мальчика имеется денег ( х – 24) копеек, а у другого ( х – 2) копеек. При сложении своих денег они все равно не смогли купить линейку. Составим простое неравенство:
( x – 24) + ( x – 2) < x.
Преобразуем его:
x – 24 + х – 2 < х ,
2 х – 26 < х ,
2 х – х < 26,
х < 26.
Итак, линейка стоит меньше 26 копеек, но больше 24 копеек, так как по условию у одного мальчика не хватает до ее стоимости 24 копеек. Линейка стоит 25 копеек.
45. Надо спросить любого депутата: «Вы консерватор?» Если он ответил «да», то сегодня четное число, а если «нет», то нечетное. По четным числам консерваторы скажут правдивое «да», а либералы, говоря неправду, тоже произнесут «да». По нечетным числам, наоборот, консерваторы, отвечая на вопрос, скажут «нет», но либералы, говорящие в эти дни только правду, тоже скажут «нет».
46. На первый взгляд кажется, что бутылка стоит 1 рубль, а пробка – 10 копеек, но тогда бутылка дороже пробки на 90 копеек, а не на 1 рубль, как по условию. На самом деле, бутылка стоит 1 рубль 05 копеек, а пробка стоит 5 копеек.
47. Может показаться, что Оля проходит 30 ступенек – в 2 раза меньше, чем Катя (так как она живет в 2 раза ниже). На самом деле это не так. Когда Катя поднимается на четвертый этаж, она преодолевает 3 лестничных пролета между этажами. Значит, между двумя этажами 20 ступенек: 60: 3 = 20. Оля поднимается с первого этажа на второй, следовательно, она преодолевает 20 ступенек.
48. Это число 91, которое при переворачивании вверх ногами превращается в 16. При этом оно уменьшается на 75 (поскольку 91–16 = 75). При решении этой задачи надо учитывать, что при переворачивании числа его цифры не только переворачиваются, но и меняются местами.
49. На развернутом листе будет 128 дырок. Надо принять во внимание, что при каждом складывании листа количество дырок удваивается.
50. Три человека: дед, отец и сын – это два отца и два сына – поймали трех зайцев, каждый по одному.
51. Эффект этой задачи-фокуса заключается в том, что увеличение любого трехзначного числа до шестизначного путем его дублирования равносильно умножению этого трехзначного числа на 1001. Кроме того, произведение чисел 13, 11 и 7 также равно 1001. Следовательно, если получившееся шестизначное число разделить в любой последовательности на эти три числа (13, 11, 7), то получится исходное трехзначное число.
52. См. рис. 59.
Читать дальше
Конец ознакомительного отрывка
Купить книгу


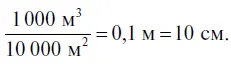
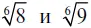 . Корень шестой степени из девяти немного больше такого же корня из восьми, следовательно,
. Корень шестой степени из девяти немного больше такого же корня из восьми, следовательно, 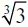 больше, чем
больше, чем 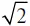 .
.










