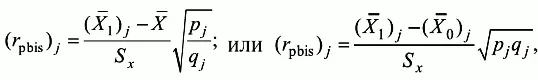Виктор Звонников - Контроль качества обучения при аттестации - компетентностный подход

Таким образом, дистракторы, которые выбирают менее 5% неверно ответивших испытуемых, следует удалять из теста. Углубленный вариант дистракторного анализа построен на подсчете значения точечно-бисериального коэффициента корреляции для каждого дистрактора в заданиях теста. Отрицательные значения коэффициента корреляции указывают на ситуацию, когда хорошо выполнившие тест испытуемые не будут выбирать данный дистрактор в качестве правильного ответа.

Значения коэффициента точечно-бисериальной корреляции для примера из табл. 6.6 приводятся в табл. 6.7 (как и ранее, звездочка соответствует правильному ответу).

Таблица 6.7 Значения коэффициента точечно-бисериальной корреляции для дистракторов

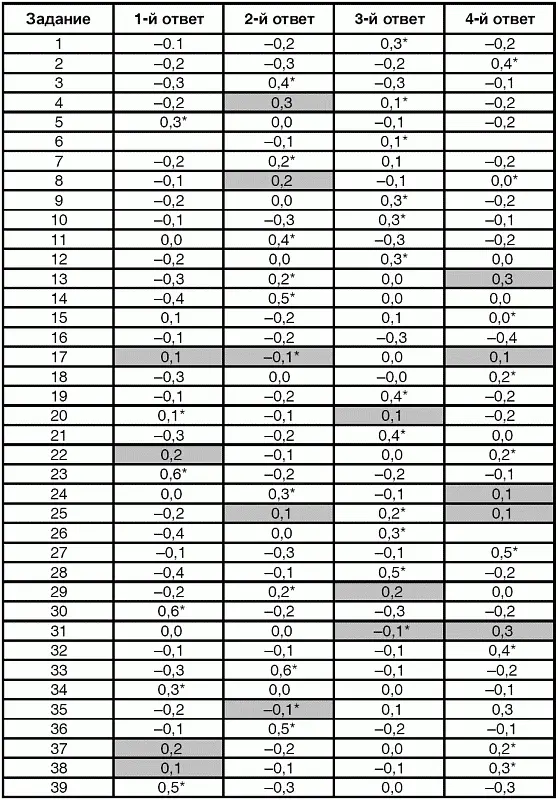
Выделенные положительные значения коэффициента точечно-бисериальной корреляции для дистракторов (например 2-й ответ в задании 4, 2-й ответ в задании 8, 4-й в 13 и т. д.) указывают на то, что эти неверные ответы выбирают в качестве правильных сильные студенты, что недопустимо в хороших заданиях теста. При правильном положении вещей значения коэффициента точечно-бисериальной корреляции для дистракторов должны быть отрицательными и превышающими по модулю 0,2. Положительные или близкие к нулю значения коэффициента для дистракторов говорят о необходимости их исключения либо переделки неправильных ответов.

Правильные ответы, наоборот, должны выбирать сильные студенты, поэтому в хороших заданиях значения коэффициента точечно-бисериальной корреляции на месте ответов со звездочкой бывают только положительными и превышающими 0,5. Для случая, когда правильный ответ не выбирают сильные студенты (например, в задании 31 или в заданиях 17, 35 из табл. 6.7), коэффициент корреляции бывает близким к нулю или даже меньше нуля. Отрицательная или нулевая корреляция для верного ответа может отражать случайный характер ответов студентов, наличие систематических проблем в усвоении проверяемого материала, вызванных дефектами преподавания либо некорректной формулировкой задания теста.

Дискриминативностью (discriminatory power) называется способность задания дифференцировать студентов на лучших и худших. Высокая дискриминативность – важная характеристика удачного тестового задания, она определяет меру валидности задания, его адекватность целям создания теста. Поэтому хороший нормативно-ориентированный тест должен быть составлен из заданий с высокой дискриминативной способностью. Для критериально-ориентированных тестов дискриминативность не является решающим фактором при отборе заданий в тест, но в любом случае невалидные задания должны быть удалены из теста.

Для оценки дискриминативности задания применяются различные формулы. Наиболее простым является расчет по формуле r дис j = p 1 j – p 0 j , где r дис j – индекс дискриминативности для j -го задания теста; p 1 j – доля студентов, правильно выполнивших j -е задание в подгруппе из 27% лучших студентов по результатам выполнения теста; p 0 j – доля студентов, правильно выполнивших j -е задание в подгруппе из 27% худших студентов по результатам выполнения теста.

Значения индекса r дисдля заданий теста обычно представляют собой десятичную дробь, принадлежащую интервалу [–1; 1]. Максимального значения 1,00 r дисдостигнет в том случае, когда все студенты из подгруппы лучших верно выполнят j -е задание теста, а из подгруппы худших это задание не выполнит верно ни один студент. Тогда задание будет обладать максимальным дифференцирующим эффектом. Нулевого значения r дисдостигнет в том случае, когда в обеих подгруппах будут равны доли студентов, правильно выполнивших j -е задание теста. И наконец, минимальное значение r дис= –1 будет в ситуации, когда данное задание теста все сильные студенты сделали неверно, а все слабые – верно. Естественно, что задания второго и третьего типа с r дис= 0 или r дис< 0 из теста следует удалить.

Более точное представление о дискриминативной способности задания можно составить, подсчитав точечный бисериальный коэффициент ( r pbis) корреляции, процесс вычисления значений которого подробно рассмотрен выше в этом же разделе. Помимо приведенной формулы для r pbis, можно использовать другие, дающие близкие значения:

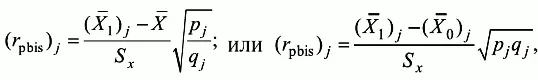
где ( r pbis) j – точечно-бисериальный коэффициент корреляции для j -го задания; ( X̅ 1) j — среднее значение индивидуальных баллов студентов, выполнивших верно j -е задание; ( X̅ 0) j — среднее значение индивидуальных баллов учеников, выполнивших j -е задание неверно; X̅ — среднее значение баллов по всей выборке студентов; S x — стандартное отклонение по множеству индивидуальных баллов.