Виктор Звонников - Контроль качества обучения при аттестации - компетентностный подход

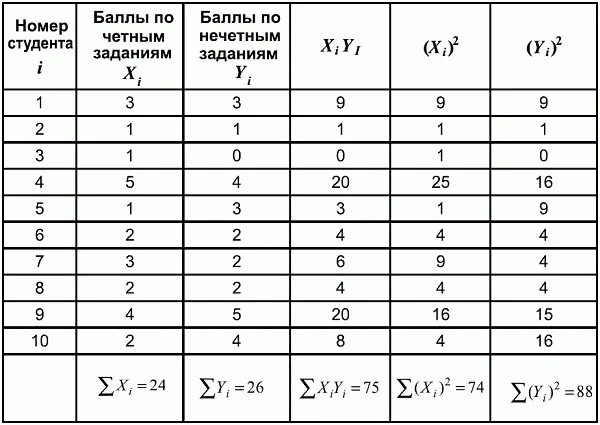
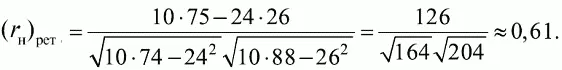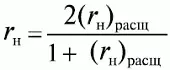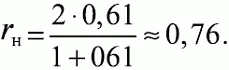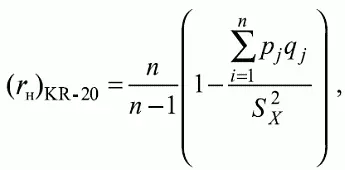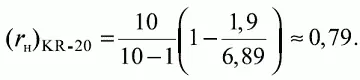Для оценивания надежности методом расщепления результаты студентов заносят в табл. 6.11.

Таблица 6.11 Сводная таблица для оценки надежности (метод расщепления)

Далее для таблицы данных используют формулу (6.9), в которой роль результатов в первом тестировании выполняют данные по четным заданиям, а во втором – по нечетным.

Пример подсчета по данным исходной матрицы приведен в табл. 6.2. Результаты испытуемых по четным и нечетным заданиям приводятся в табл. 6.12.

После подстановки чисел из табл. 6.12 в формулу (6.9) получается

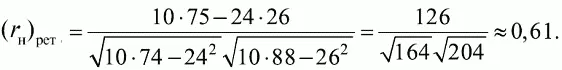
По сравнению с прежним значением 0,78 надежность получилась намного меньше, что можно было предвидеть, поскольку тест укоротился в два раза (после расщепления подсчет надежности был по пяти заданиям вместо десяти).

Таблица 6.12 Пример подсчета надежности методом расщепления

Для коррекции оценки надежности в соответствии с длиной исходного теста используется формула Спирмена–Брауна

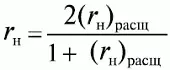
где в числителе и знаменателе дроби стоит коэффициент надежности для половины заданий теста, а слева скорректированный коэффициент надежности с учетом всех заданий теста.

Тогда для рассматриваемого примера коэффициент надежности теста из десяти заданий будет

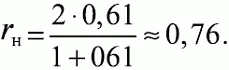
После коррекции коэффициент надежности получился приблизительно такой же, как и в предыдущем случае подсчета ретестовым методом ( r н= 0,78). Применение формулы Спирмена–Брауна подтверждает высказанное ранее предположение: увеличение длины повышает надежность теста.

Приведенный метод оценивания надежности имеет свои ограничения в применении. Он основан на допущении параллельности двух половин теста, что не всегда и не в полной мере может оказаться верным. Корреляция двух половин возрастает по мере роста гомогенности теста. В этой связи метод расщепления нередко называют методом оценки внутренней состоятельности (согласованности) теста (Internal-Consistency Method).

Метод Кьюдера-Ричардсона для оценки надежности также основан на однократном тестировании, но в отличие от предыдущего подхода не зависит от искусственных допущений о полной параллельности двух частей теста. Однако и он имеет свою ограниченную сферу применения, поскольку годится исключительно при использовании дихотомических оценок по результатам выполнения заданий гомогенных тестов.

Формула Кьюдера-Ричардсона (F. Kuder, M. Richardson-20, или KR-20) имеет вид [28, 36]

(6.10)

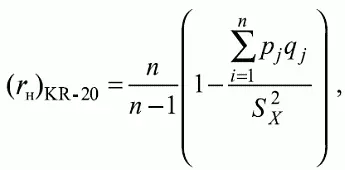
где р j – доля правильных ответов на j -е задание; q j — доля неправильных ответов, q j = 1 – р j ; S X 2 — дисперсия по распределению наблюдаемых баллов; n — число заданий теста.

Для исходной матрицы данных подсчитанная ранее исправленная дисперсия S X 2 = 6,89 , а доли правильных ответов получаются делением чисел R j в последней строке матрицы на 10. Тогда сумма произведений долей правильных и неправильных ответов будет 0,9 · 0,1 + 0,8 · 0,2 + 0,7 · 0,3 + 0,6 · 0,4 + 0,5 · 0,5+ 0,5 · 0,5 + 0,3 · 0,7 + 0,4 · 0,6 + 0,2 · 0,8 + 0,1 · 0,9 = 1,9 и коэффициент надежности

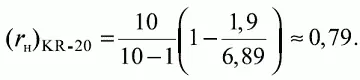
При оценке надежности нельзя полагаться лишь на один показатель, поскольку каждый из них имеет свои ограничения, смещающие оценки надежности теста в сторону завышения или занижения. Для достоверной проверки качества теста следует учитывать несколько показателей надежности, подсчитанных по разным формулам, лишь небольшая часть которых приведена в данном тексте. В качестве нижнего предела допустимых значений надежности обычно выбирают 0,7. При более низком значении использование теста вряд ли целесообразно в силу большой погрешности измерения.