Виктор Звонников - Контроль качества обучения при аттестации - компетентностный подход

Рис. 2.5. Иллюстрация связи переменных при одномерном измерении

Чтобы принять гипотезу об одномерности теста, необходимо выявить связь между теоретическим конструктом и эмпирическими индикаторами, роль которых выполняют задания теста. Оценка связи требует ответа на вопрос: есть ли разница между доказательством одномерности конструкта и доказательством одномерности заданий теста?

На рис. 2.6 приведена измерительная модель для одномерного случая, иллюстрирующая связь между конструктом, обозначенным символом T , и четырьмя заданиями ( x 1, x 2, x 3, x 4). Числа, стоящие у каждого луча, показывают меру предполагаемой корреляционной связи между конструктом и заданиями теста.

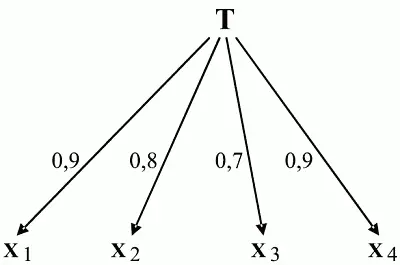
Рис. 2.6. Измерительная модель, иллюстрирующая связь между конструктом и заданиями теста (одномерный случай)

При анализе модели важно понимать, что конструкт является латентным (скрытым от возможностей непосредственного измерения) фактором, взаимодействие которого с заданиями порождает наблюдаемые результаты выполнения теста. Влияние конструкта, включающего одну или несколько латентных переменных измерения, на эмпирические индикаторы отражено на рассматриваемом рисунке с помощью направленных лучей.

Гипотетическая корреляционная матрица, показывающая меру связей между конструктом и заданиями теста, помещена в табл. 2.1. В силу симметрии чисел в матрице относительно главной диагонали, состоящей из единиц, таблица имеет треугольный вид.

Таблица 2.1 Значения корреляции между заданиями

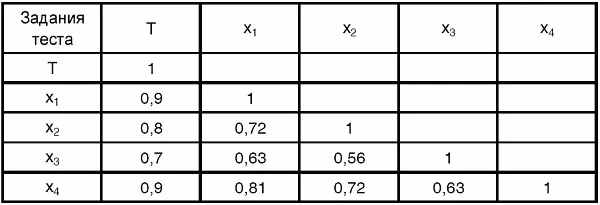
Для анализа связи между размерностью конструкта и размерностью тестовых заданий, используемых при оценивании наблюдаемых переменных, необходимо подсчитать частные корреляции, получаемые путем удаления влияния на парные корреляции третьей переменной. Используя величины корреляций в табл. 2.1 и упомянутый подход, можно показать, что частная корреляция между любой парой наблюдаемых переменных x 1, x 2, x 3после удаления влияния латентной переменной T будет равна нулю.

Аналогичные вычисления можно провести для любой пары наблюдаемых переменных x 1, x 2, x 3. Интерпретируя полученные нулевые результаты для анализа связи переменных, можно утверждать, что после удаления эффекта влияния фактора T связь между наблюдаемыми переменными исчезает. Таким образом, латентный фактор T является единственной переменной, связывающей наблюдаемые переменные x 1, x 2, x 3, поэтому его следует трактовать как единственный общий фактор для совокупности наблюдаемых переменных. Отсюда следует вывод об одномерности совокупности заданий x 1– x 3, поскольку корреляция между ними после удаления влияния общего фактора становится равной нулю.

Подобный концептуальный подход к доказательству одномерности был предложен Макдональдом и Хати (McDonald, 1981; Hattie, 1985) [38]. Конечно, на практике при анализе размерности пространства измерений говорить о точном равенстве нулю частных корреляций не приходится в силу влияния различных ошибок измерения. Однако в случае близких к нулю значений частных корреляций по результатам педагогических измерений можно строить единственную шкалу. Поскольку каждое задание в рассмотренном гипотетическом примере измеряет один и только один конструкт, то справедлив вывод об одномерности заданий теста. Обратный вывод в общем случае не верен: из одномерности заданий не следует одномерность теста. Совокупность одномерных заданий, каждое из которых измеряет свой конструкт, не означает наличия общего единственного фактора, свидетельствующего об одномерности пространства измерений.

Если конструкт включает не одну, а несколько переменных, то измерения называют многомерными. Такая ситуация как раз характерна при разработке и использовании компетентностных тестов. Совокупность переменных образует пространство переменных измерения, размерность которого равна их числу. Геометрическая интерпретация двумерных измерений приведена на рис. 2.7. Рисунок изображает частный случай, когда каждая из латентных переменных F 1 и F 2 воздействует на обе наблюдаемые переменные Х 1и Х 2, находящиеся под влиянием ошибок измерения E 1и E 2.