Нассим Талеб - The Black Swan. The Impact of the Highly Improbable

Poisson jump: Sometimes people propose a Gaussian distribution with a small probability of a “Poisson” jump. This may be fine, but how do you know how large the jump is going to be? Past data might not tell you how large the jump is.

Small sample effect: Weron (2001). Officer (1972) is quite ignorant of the point.

Recursivity of statistics: Taleb and Pilpel (2004), Blyth et al. (2005).

Biology: Modern molecular biology pioneers Salvador Luria and Max Delbrück witnessed a clustering phenomenon with the occasional occurrence of extremely large mutants in a bacterial colony, larger than all other bacteria.

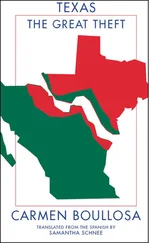
Thermodynamics: Entropy maximization without the constraints of a second moment The two exhaustive domains of attraction: vertical or straight line with slopes either negative infinity or constant negative α. Note that since probabilities need to add up to 1 (even in France) there cannot be other alternatives to the two basins, which is why I narrow it down to these two exclusively.

FIGURE 15: TYPICAL DISTRIBUTION WITH POWER-LAW TAILS (HERE A STUDENT T)

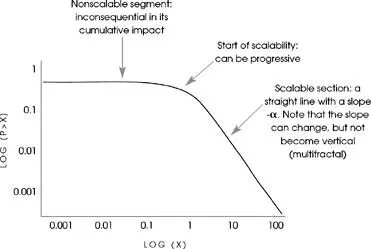
FIGURE 16

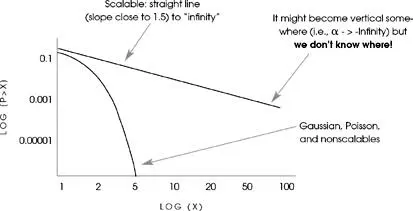
My ideas are made very simple with this clean cut polarization—added to the problem of not knowing which basin we are in owing to the scarcity of data on the far right. leads to a Levy-stable distribution—Mandelbrot’s thesis of 1952 (see Mandelbrot [1997a]). Tsallis’s more sophisticated view of entropy leads to a Student T.

Imitation chains and pathologies: An informational cascade is a process where a purely rational agent elects a particular choice ignoring his own private information (or judgment) to follow that of others. You run, I follow you, because you may be aware of a danger I may be missing. It is efficient to do what others do instead of having to reinvent the wheel every time. But this copying the behavior of others can lead to imitation chains. Soon everyone is running in the same direction, and it can be for spurious reasons. This behavior causes stock market bubbles and the formation of massive cultural fads. Bikhchandani et al. (1992). In psychology, see Hansen and Donoghue (1977). In biology/selection, Dugatkin (2001), Kirpatrick and Dugatkin (1994).

Self-organized criticality: Bak and Chen (1991), Bak (1996).

Economic variables: Bundt and Murphy (2006). Most economic variables seem to follow a “stable” distribution. They include foreign exchange, the GDP, the money supply, interest rates (long and short term), and industrial production.

Statisticians not accepting scalability: Flawed reasoning mistaking for sampling error in the tails for a boundedness: Perline (2005), for instance, does not understand the difference between absence of evidence and evidence of absence.

Time series and memory: You can have “fractal memory,” i.e., the effect of past events on the present has an impact that has a “tail.” It decays as power-law, not exponentially.

Marmott’s work: Marmott (2004).

CHAPTER 18

Economists: Weintraub (2002), Szenberg (1992).

Portfolio theory and modern finance: Markowitz (1952, 1959), Huang and Litzenberger (1988) and Sharpe (1994, 1996). What is called the Sharpe ratio is meaningless outside of Mediocristan. The contents of Steve Ross’s book (Ross [2004]) on “neoclassical finance” are completely canceled if you consider Extremistan in spite of the “elegant” mathematics and the beautiful top-down theories. “Anecdote” of Merton minor in Merton (1992).

Obsession with measurement: Crosby (1997) is often shown to me as convincing evidence that measuring was a great accomplishment not knowing that it applied to Mediocristan and Mediocristan only. Bernstein (1996) makes the same error.

Power laws in finance: Mandelbrot (1963), Gabaix et al. (2003), and Stanley et al. (2000). Kaizoji and Kaizoji (2004), Véhel and Walter (2002). Land prices: Kaizoji (2003). Magisterial: Bouchaud and Potters (2003).

Equity premium puzzle: If you accept fat tails, there is no equity premium puzzle. Benartzi and Thaler (1995) offer a psychological explanation, not realizing that variance is not the measure. So do many others.

Covered writes: a sucker’s game as you cut your upside—conditional on the upside being breached, the stock should rally a lot more than intuitively accepted. For a representative mistake, see Board et al. (2000).

Nobel family: “Nobel Descendant Slams Economics Prize,” The Local , September 28, 2005, Stockholm.

Double bubble: The problem of derivatives is that if the underlying security has mild fat tails and follows a mild power law (i.e., a tail exponent of three or higher), the derivative will produce far fatter tails (if the payoff is in squares, then the tail exponent of the derivatives portfolio will be half that of the primitive). This makes the Black-Scholes-Merton equation twice as unfit!

Poisson busting: The best way to figure out the problems of the Poisson as a substitute for a scalable is to calibrate a Poisson and compute the errors out of sample. The same applies to methods such as GARCH—they fare well in sample, but horribly, horribly outside (even a trailing three-month past historical volatility or mean deviation will outperform a GARCH of higher orders).

Why the Nobel: Derman and Taleb (2005), Haug (2007).

Claude Bernard and experimental medicine: “Empiricism pour le présent, avec direction a aspiration scientifique pour l’avenir.” From Claude Bernard, Principe de la médecine expérimentale . See also Fagot-Largeault (2002) and Ruffié (1977). Modern evidence-based medicine: Ierodiakonou and Vandenbroucke (1993) and Vandenbroucke (1996) discuss a stochastic approach to medicine.

CHAPTER 19

Popper quote: From Conjectures and Refutations , pages 95–97.

The lottery paradox: This is one example of scholars not understanding the high-impact rare event. There is a well-known philosophical conundrum called the “lottery paradox,” originally posed by the logician Henry Kyburg (see Rescher [2001] and Clark [2002]), which goes as follows: “I do not believe that any ticket will win the lottery, but I do believe that all tickets will win the lottery.” To me (and a regular person) this statement does not seem to have anything strange in it. Yet for an academic philosopher trained in classical logic, this is a paradox. But it is only so if one tries to squeeze probability statements into commonly used logic that dates from Aristotle and is all or nothing . An all or nothing acceptance and rejection (“I believe” or “I do not believe”) is inadequate with the highly improbable. We need shades of belief, degrees of faith you have in a statement other than 100% or 0%.

One final philosophical consideration. For my friend the options trader and Talmudic scholar Rabbi Tony Glickman: life is convex and to be seen as a series of derivatives. Simply put, when you cut the negative exposure, you limit your vulnerability to unknowledge, Taleb (2005).