Networks: Barabási and Albert (1999), Albert and Barabási (2000), Strogatz (2001, 2003), Callaway et al. (2000), Newman et al. (2000), Newman, Watts, and Strogatz (2000), Newman (2001), Watts and Strogatz (1998), Watts (2002, 2003), and Amaral et al. (2000). It supposedly started with Milgram (1967). See also Barbour and Reinert (2000), Barthélémy and Amaral (1999). See Boots and Sasaki (1999) for infections. For extensions, see Bhalla and Iyengar (1999). Resilence, Cohen et al. (2000), Barabási and Bonabeau (2003), Barabási (2002), and Banavar et al. (2000). Power laws and the Web, Adamic and Huberman (1999) and Adamic (1999). Statistics of the Internet: Huberman (2001), Willinger et al. (2004), and Faloutsos, Faloutsos, and Faloutsos (1999). For DNA, see Vogelstein et al. (2000).
Self-organized criticality: Bak (1996).
Pioneers of fat tails: For wealth, Pareto (1896), Yule (1925, 1944). Less of a pioneer Zipf (1932, 1949). For linguistics, see Mandelbrot (1952).
Pareto: See Bouvier (1999).
Endogenous vs. exogenous: Sornette et al. (2004).
Sperber’s work: Sperber (1996a, 1996b, 1997).
Regression: If you hear the phrase least square regression , you should be suspicious about the claims being made. As it assumes that your errors wash out rather rapidly, it underestimates the total possible error, and thus overestimates what knowledge one can derive from the data.
The notion of central limit: very misunderstood: it takes a long time to reach the central limit—so as we do not live in the asymptote, we’ve got problems. All various random variables (as we started in the example of Chapter 16 with a +1 or −1, which is called a Bernouilli draw) under summation (we did sum up the wins of the 40 tosses) become Gaussian. Summation is key here, since we are considering the results of adding up the 40 steps, which is where the Gaussian, under the first and second central assumptions becomes what is called a “distribution.” (A distribution tells you how you are likely to have your outcomes spread out, or distributed.) However, they may get there at different speeds. This is called the central limit theorem: if you add random variables coming from these individual tame jumps, it will lead to the Gaussian.
Where does the central limit not work? If you do not have these central assumptions, but have jumps of random size instead, then we would not get the Gaussian. Furthermore, we sometimes converge very slowly to the Gaussian. For preasymptotics and scalability, Mandelbrot and Taleb (2007a), Bouchaud and Potters (2003). For the problem of working outside asymptotes, Taleb (2007).
Aureas mediocritas: historical perspective, in Naya and Pouey-Mounou (2005) aptly called Éloge de la médiocrité .
Reification (hypostatization): Lukacz, in Bewes (2002).
Catastrophes: Posner (2004).
Concentration and modern economic life: Zajdenweber (2000).
Choices of society structure and compressed outcomes: The classical paper is Rawls (1971), though Frohlich, Oppenheimer, and Eavy (1987a, 1987b), as well as Lissowski, Tyszka, and Okrasa (1991), contradict the notion of the desirability of Rawl’s veil (though by experiment). People prefer maximum average income subjected to a floor constraint on some form of equality for the poor, inequality for the rich type of environment.
Gaussian contagion: Quételet in Stigler (1986). Francis Galton (as quoted in Ian Hacking’s The Taming of Chance) : “I know of scarcely anything so apt to impress the imagination as the wonderful form of cosmic order expressed by ‘the law of error.’”
“Finite variance” nonsense: Associated with CLT is an assumption called “finite variance” that is rather technical: none of these building-block steps can take an infinite value if you square them or multiply them by themselves. They need to be bounded at some number. We simplified here by making them all one single step, or finite standard deviation. But the problem is that some fractal payoffs may have finite variance, but still not take us there rapidly. See Bouchaud and Potters (2003).
Lognormal: There is an intermediate variety that is called the lognormal, emphasized by one Gibrat (see Sutton [1997]) early in the twentieth century as an attempt to explain the distribution of wealth. In this framework, it is not quite that the wealthy get wealthier, in a pure preferential attachment situation, but that if your wealth is at 100 you will vary by 1, but when your wealth is at 1,000, you will vary by 10. The relative changes in your wealth are Gaussian. So the lognormal superficially resembles the fractal, in the sense that it may tolerate some large deviations, but it is dangerous because these rapidly taper off at the end. The introduction of the lognormal was a very bad compromise, but a way to conceal the flaws of the Gaussian.
Extinctions: Sterelny (2001). For extinctions from abrupt fractures, see Courtillot (1995) and Courtillot and Gaudemer (1996). Jumps: Eldredge and Gould.
FRACTALS, POWER LAWS, and SCALE-FREE DISTRIBUTIONS
Definition: Technically, P>x= K x -α where α is supposed to be the power-law exponent. It is said to be scale free, in the sense that it does not have a characteristic scale: relative deviation of 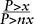 does not depend on x, but on n—for x “large enough.” Now, in the other class of distribution, the one that I can intuitively describe as nonscalable, with the typical shape p(x) = Exp[-a x], the scale will be a.
does not depend on x, but on n—for x “large enough.” Now, in the other class of distribution, the one that I can intuitively describe as nonscalable, with the typical shape p(x) = Exp[-a x], the scale will be a.
Problem of “how large”: Now the problem that is usually misunderstood. This scalability might stop somewhere, but I do not know where, so I might consider it infinite. The statements very large and I don’t know how large and infinitely large are epistemologically substitutable. There might be a point at which the distributions flip. This will show once we look at them more graphically.
Log P>x = -α Log X +C tfor a scalable. When we do a log-log plot (i.e., plot P>x and x on a logarithmic scale), as in Figures 15 and 16, we should see a straight line.
Fractals and power laws: Mandelbrot (1975, 1982). Schroeder (1991) is imperative. John Chipman’s unpublished manuscript The Paretian Heritage (Chipman [2006]) is the best review piece I’ve seen. See also Mitzenmacher (2003).
“To come very near true theory and to grasp its precise application are two very different things as the history of science teaches us. Everything of importance has been said before by somebody who did not discover it.” Whitehead (1925).
Fractals in poetry: For the quote on Dickinson, see Fulton (1998).
Lacunarity: Brockman (2005). In the arts, Mandelbrot (1982).
Fractals in medicine: “New Tool to Diagnose and Treat Breast Cancer,” Newswise , July 18, 2006.
General reference books in statistical physics: The most complete (in relation to fat tails) is Sornette (2004). See also Voit (2001) or the far deeper Bouchaud and Potters (2002) for financial prices and econophysics. For “complexity” theory, technical books: Bocarra (2004), Strogatz (1994), the popular Ruelle (1991), and also Prigogine (1996).
Fitting processes: For the philosophy of the problem, Taleb and Pilpel (2004). See also Pisarenko and Sornette (2004), Sornette et al. (2004), and Sornette and Ide (2001).
Читать дальше

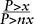 does not depend on x, but on n—for x “large enough.” Now, in the other class of distribution, the one that I can intuitively describe as nonscalable, with the typical shape p(x) = Exp[-a x], the scale will be a.
does not depend on x, but on n—for x “large enough.” Now, in the other class of distribution, the one that I can intuitively describe as nonscalable, with the typical shape p(x) = Exp[-a x], the scale will be a.