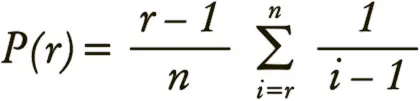Ханна Фрай - Математика любви. Закономерности, доказательства и поиск идеального решения

Если поставить себе такие ограничения, то область математики, которая называется “теория оптимальной остановки случайного процесса”, может предложить наилучшую стратегию поиска того самого “кандидата номер один”, несравненного Прекрасного принца (или Принцессы). Ход рассуждений тут самый простой и логичный: пока вы молоды, играйте в свое удовольствие, не рассматривая никого в качестве спутника жизни, пока окончательно не освоитесь на этой “игровой площадке”. Когда этот этап (назовем его “фазой отвержения”) будет пройден, выбирайте первого, кто ответит на ваши чувства и кто при этом будет лучше, чем любой из ваших предыдущих партнеров.

Однако теория оптимальной остановки идет дальше. Оказывается, что вероятность того, что вы остановитесь, остепенитесь и останетесь с лучшим из возможных партнером (эта вероятность обозначена в уравнении буквой P ), зависит от числа ваших потенциальных спутников жизни ( n ) и от того, скольким из них вы уже отказали ( r ), и эта зависимость описывается довольно элегантной формулой:

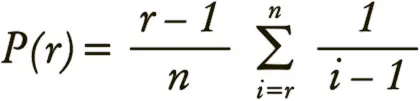
Эта формула, на вид вполне невинная, в состоянии объяснить, сколько претендентов вы должны отвергнуть, прежде чем ваши шансы обрести идеального партнера станут максимальными. Например, если вам на роду написаны десять партнеров за всю жизнь, то наибольшая вероятность найти вашего Единственного и Неповторимого возникает после того, как вы отвергли первых четырех поклонников (и эта вероятность составляет 39,87 %). Если вам суждено встретиться с двадцатью потенциальными спутниками, вы должны отказать первым восьми (и в 38,42 % случаев следующим будет мистер или мисс Совершенство).

И, наконец, если ваша судьба – бесконечное число партнеров, вы должны отклонить первые 37 % – и тогда ваши шансы на успех будут чуть больше, чем один к трем [9]. Я математик, и поэтому, конечно, человек предвзятый, но, признаюсь, от этого результата у меня буквально срывает крышу.

Если вы отвергнете эту стратегию и решите просто остановиться на случайно выбранном партнере из своего списка, то шанс, что это окажется ваша истинная любовь, составляет 1/n, то есть 5 % (в случае, если вам за всю жизнь предназначено вступить в отношения с двадцатью партнерами). Однако, просто отвергнув 37 % из своих двадцати партнеров, вы можете коренным образом изменить судьбу, увеличив свои шансы до впечатляющих 38,42 %!

Хорошо-хорошо, пока меня окончательно не занесло: конечно, вы могли заметить, что если попытаться приложить этот план к настоящим человеческим отношениям, в нем обнаружатся определенные изъяны. Если вы не член английской королевской семьи XVI века, то ваши потенциальные женихи или невесты не будут заранее выстраиваться в длинную очередь. Кроме того, нет ни малейшей возможности узнать, со сколькими людьми вы могли бы завязать отношения в течение всей своей жизни. И если вас зовут не Хью Хефнер, вы, вероятно, не планируете иметь бесконечно большое число сексуальных партнеров.

К счастью, есть и другой вариант этой задачи, который гораздо больше подходит для простых смертных, таких, как вы и я, и позволяет получить столь же впечатляющий результат. В этом варианте вам совершенно не обязательно гадать, сколько партнеров вы могли бы встретить за всю свою жизнь – достаточно знать, как долго вы планируете вести свободный образ жизни, прежде чем решите остепениться. Расчеты в этом случае намного сложнее [10], хотя в конце вновь всплывает тот же результат – 37 %. Только на этот раз он относится не к количеству претендентов, а ко времени.

Допустим, вы начали бегать на свидания в пятнадцать лет и в идеале хотели бы остепениться и завести семью к сорока. Назовем эти двадцать пять лет “окном свиданий”. В течение первых 37 % этого срока (то есть примерно пока вам не стукнет двадцать четыре) вы должны отказывать всем, кто предлагает вам любовь до гроба. Используйте это время, чтобы понять, что к чему и, главное, разобраться, чего, в сущности, вы хотите от будущего спутника жизни. Когда этот этап закончится, выбирайте первого, кто окажется лучше всех предыдущих.

Эта стратегия даст вам наилучший шанс найти партнера номер один из вашего воображаемого списка. Но предупреждаю: даже этот вариант имеет свои недостатки.