Ханна Фрай - Математика любви. Закономерности, доказательства и поиск идеального решения

В большинстве случаев мы решаем эту проблему следующим образом: рассылаем приглашения, а затем корректируем список по мере того, как приходят ответы с подтверждением или отказом и извинениями. Но можно ли считать такой подход безопасным в наш век, когда люди считают, что их завтрак – вполне достаточный повод обновить статус в Facebook ? Весть о том, что вы рассылаете приглашения, мгновенно разнесется среди знакомых, и друзья и родственники “второго ряда” обидятся, что не были включены в почетный “ближний круг”.

В качестве альтернативного метода вы можете просто пригласить меньшее число гостей или отложить аренду зала для торжества до того момента, когда вы будете знать точное число участников. А можно, как делают многие, просто попытаться угадать вслепую.

Однако есть один математический способ, который позволит вам обрести почву под ногами, пока не начались ссоры с будущими тещами и свекрами.

Начнем с того, что составим список всех потенциальных гостей, сгруппируем его по парам или семьям, а затем отсортируем эти группы по степени значимости их присутствия на свадьбе. Эта задача может показаться неразрешимой, но если вы сами не знаете, кто из ваших друзей нравится вам больше, а кто меньше, то тут и математика не поможет.

Итак, превращаем наш список в электронную таблицу, где в первой колонке будут названия групп гостей, во второй – число людей в группе.

Теперь по каждой группе нужно оценить вероятность того, что эти ваши друзья действительно появятся, если вы их пригласите. Как далеко они живут? Что сейчас происходит в их жизни? А может быть, в глубине души они вас терпеть не могут? В общем, разбирайтесь.

Мысленно давайте оценку в процентах, но в таблицу записывайте вероятность в десятичной дроби. Например, если ваша близкая подруга со своим бойфрендом придут с вероятностью 95 %, то в таблицу напротив их имен вы записываете число 0,95.

Умножив цифру из второй колонки (число людей в каждой группе) на вероятность появления группы (третья колонка), вы получите четвертую колонку – ожидаемое количество гостей на свадьбе.

Двигаясь по списку сверху вниз, от VIP -персон к вечным аутсайдерам, записывайте в пятой колонке число гостей (каждый раз прибавляя результат из соответствующей строки колонки № 4). Самый простой способ завершить подсчет – отсечь ту часть списка, которая останется, когда число в пятой колонке превысит число мест за столами в зале, который вы арендуете для мероприятия.

Примером того, как может выглядеть нижняя часть списка, может служить эта таблица:

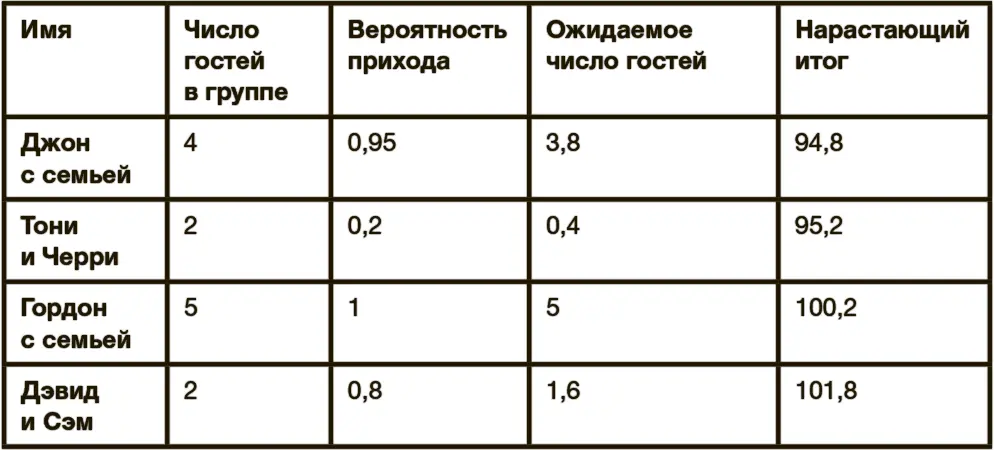
Если вы планируете принять сто гостей, то можете пригласить всех, включая Гордона с семьей (у вас получится чуть больше сотни приглашенных, но в среднем можно ожидать, что придут как раз сто). К сожалению, на этот раз Дэвид и Сэм не вышли в финал (может быть, это и к лучшему).

Внимательный читатель, конечно, уже заметил недостаток этого метода. Поскольку мы имеем дело с вероятностями, не исключено, что согласием ответят как больше ста человек, так и меньше. Во втором случае у вас появится возможность в последнюю минуту пригласить тех, кто остался за бортом (а также тех, о ком вы просто забыли, составляя список), но вот если придет больше людей, чем вы рассчитывали, это может стать катастрофой. Поэтому неплохо было бы сразу же рассчитать этот катастрофический сценарий, а затем ограничить список таким образом, чтобы свести к минимуму вероятность того, что мест не хватит. Но как рассчитать вероятность катастрофы?

Допустим, что для того чтобы к вам пришли сто гостей, вам нужно разослать сто пятьдесят приглашений. На самом деле число принявших приглашение может оказаться любым в интервале от 0 до 150, но вероятность обоих экстремальных значений крайне низка.

На самом деле рассчитать вероятность того, что придут все 150 приглашенных, довольно легко: нужно просто перемножить все вероятности из третьей колонки. Например, вероятность того, что придут и Джон, и Тони, и Гордон с семьями, составляет: 0,95 × 0,2 × 1,0 = 0,19, или 19 %.

Теоретически можно рассчитать вероятность прихода любого количества гостей, просто перебрав все возможные комбинации “да” и “нет” [12].

Если поместить рассчитанные вероятности для каждого числа гостей в график, то он будет выглядеть примерно так:

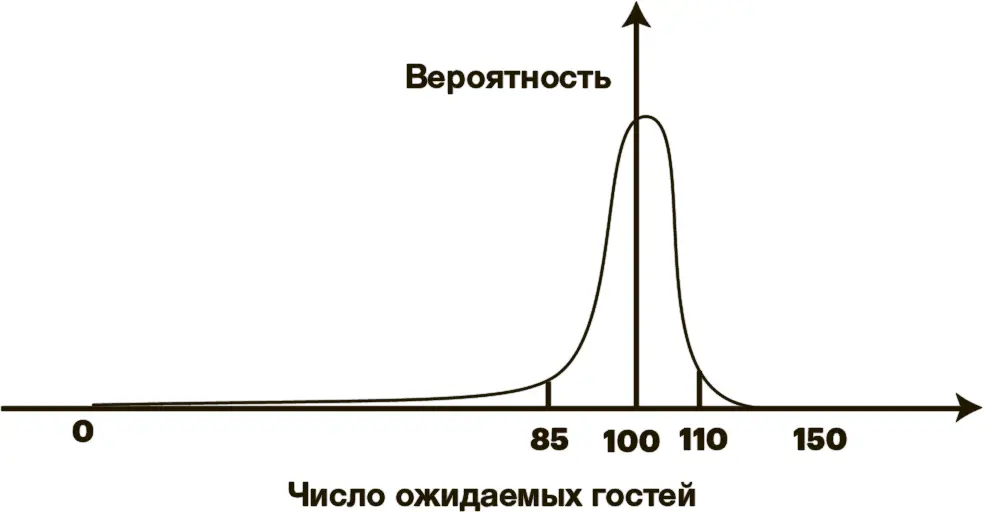
Вероятность того, что придет определенное количество гостей, резко возрастает в середине интервала, и в среднем вы можете ожидать, что придет сто человек.