Ханна Фрай - Математика любви. Закономерности, доказательства и поиск идеального решения

Как и во многих ранее проведенных опросах, выяснилось, что среднее число сексуальных партнеров в течение жизни респондентов относительно невелико: примерно семь для гетеросексуальных женщин и примерно тринадцать для гетеросексуальных мужчин. Но прежде чем мы начнем обсуждать старомодные теории о ветреных мужчинах и целомудренных женщинах, наиболее проницательные из вас удивятся: а как вообще возможно подобное несовпадение?

И в самом деле: если в мире имеется примерно поровну гетеросексуальных мужчин и женщин и если в подавляющем большинстве случаев в сексуальном акте участвуют двое, то среднее число партнеров у мужчин и у женщин должно быть примерно одинаковым. Тем не менее подобные опросы вновь и вновь выявляют приблизительно одно и то же соотношение между средними значениями числа контактов для женщин и для мужчин.

Существует несколько возможных объяснений этого факта.

Во-первых, мужчины, кажется, более склонны к преувеличениям (или “ложным ответам”, как это называется у социологов). Во-вторых, возможно, у мужчин и женщин разные критерии того, что именно должно произойти у них с партнером, чтобы они включили его в список своих сексуальных контактов.

Несколько более убедительное предположение заключается в том, что у некоторых женщин может быть необычно большое количество сексуальных партнеров, но такие женщины непропорционально представлены в выборках. Например, представьте женщину, которая признается, что у нее было 3000 мужчин. Этого было бы достаточно, чтобы среднее число партнеров для всех участниц опроса подскочило с семи до восьми (что лишний раз возвращает нас к вопросу о том, насколько адекватно среднее арифметическое описывает средние показатели).

Но, пожалуй, еще важнее то, что мужчины и женщины совершенно по-разному считают своих партнеров. Женщины, как правило, считают в хронологическом порядке, вспоминая мужчин по имени: “Ну, Гарри, потом Зейн, потом этот… Лиам”. Подобный метод подсчета дает достаточно точный результат, но если вы кого-нибудь забыли, то истинное число ваших партнеров будет преуменьшено. В то же время мужчины предпочитают округлять: “Ну, скажем… примерно по пять в год в течение последних четырех лет”. Опять же, это приемлемый метод, но с тенденцией к переоценке. В этот момент мы начинаем понимать, что поразительно большое число побед, одержанных (судя по их ответам) некоторыми мужчинами, стоит иногда поделить на пять.

Впрочем, помимо средних значений, шведское исследование предоставило нам и другие данные, позволяющие сделать поистине революционное открытие.

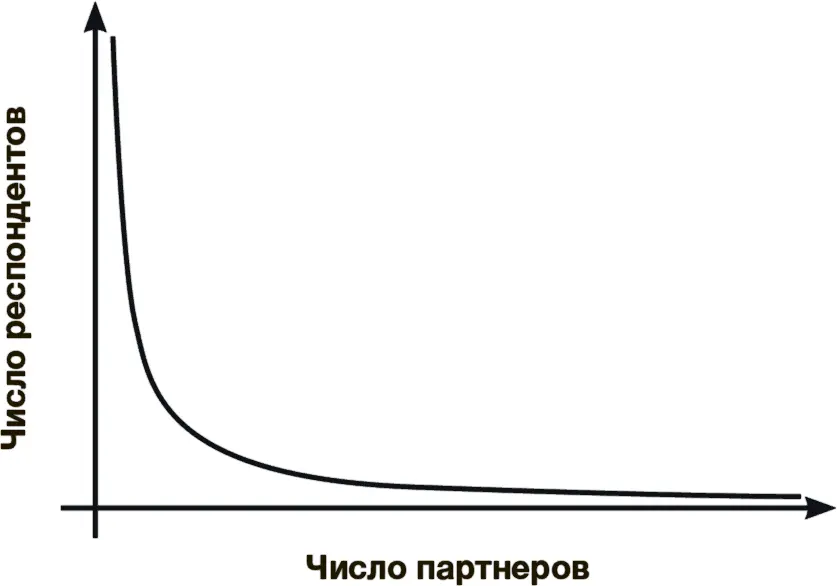
В 1999 году руководитель исследования Фредрик Лильерос и его коллеги-математики из Стокгольмского университета представили полученную ими статистику в виде графика и обнаружили поразительно простую зависимость. Почти все 2810 ответов расположились на практически идеальной кривой, как показано на рисунке ниже, продемонстрировав тем самым очевидную закономерность в распределении участников по количеству партнеров.

У подавляющего большинства опрошенных число сексуальных партнеров совсем невелико – вот почему левая часть кривой поднимается высоко вверх. Но среди респондентов было также некоторое количество людей, которые назвали необычно высокое число “побед”, поэтому правая часть кривой плавно приближается к нулевым значениям, но никогда их не достигает. Если шведский опрос репрезентативно представляет население в целом, то такой вид кривой говорит о том, что всегда есть шанс найти кого-то, у кого было сколь угодно большое число сексуальных партнеров. Понятно, что в мире не так уж много людей, у которых было, скажем, десять тысяч или даже “всего” тысяча партнеров, однако график предсказывает, что хотя бы один такой всегда может найтись.

Все это легко сворачивается в одну-единственную формулу, которая позволит предсказать, с каким количеством партнеров переспал каждый из нас. Для произвольно выбранного жителя Земли вероятность иметь больше, чем x партнеров, составляет x –α.

Параметр α рассчитывается по данным опросов. Например, исследователи определили, что для шведской женщины величина α составляет 2,1. Если это значение экстраполировать на весь мир, то вероятность того, что у кого-то было более сотни партнеров, составит 0,006 % – иными словами, это будет всего один человек из 15 800. Вероятность резко уменьшается с увеличением числа предполагаемых партнеров, тем не менее шанс найти кого-то, у кого было более тысячи партнеров, составляет 0,00005 %, то есть это один из двух миллионов человек.