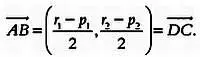Иными словами, максимальное число районов В( n ) равно сумме n и числа районов, полученных на предыдущем этапе, В( n — 1):
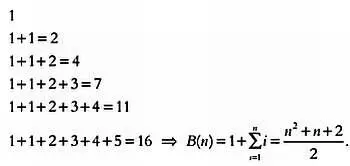
При подобном расположении улиц город будет выглядеть примерно так:

Образующаяся кривая — так называемая эвольвента В(n) для n —>  кривая — гипербола, которая описывается уравнением:
кривая — гипербола, которая описывается уравнением:
х 2 + у 2+ 2 ху — 4 у = 0.
Если же улицы необязательно должны быть прямыми, то максимально возможное число районов будет равно В( n ) = 2 n . На следующем рисунке изображен план города, который делится шестью улицами на 64 района:

Порядок среди хаоса: теорема Вариньона
Теорема Вариньона — это знаменитая теорема планиметрии, описывающая удивительный феномен. В классификации Дьёрдя Пойа это задача на доказательство.
Эта теорема иллюстрирует два важных принципа: во-первых, доказательство, которое не объясняет явление, не является достаточным, во-вторых, цель творческого подхода в математике заключается в том, чтобы понять явление, а для этого необходимо всестороннее доказательство. Иными словами, иногда «доказать» не означает «объяснить».
Выберем четыре произвольные точки плоскости Р, Q, R, S и соединим их отрезками, образуя четырехугольник. Обозначим середины его сторон точками А, В, С, D . Соединим эти точки так, чтобы получился второй четырехугольник внутри первого. Замечаете ли вы нечто особенное?
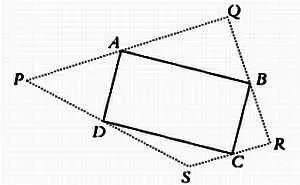
Повторите построение для других исходных точек, и вы увидите то же самое.
Перед нами — необычная ситуация. Кажется, что геометрия не подчиняется здравому смыслу. Какую бы форму ни имел исходный четырехугольник, для него всегда будет выполняться утверждение:
четырехугольник, вершины которого совпадают с серединами сторон произвольного четырехугольника, является параллелограммом.
Мы обнаружили порядок среди хаоса. Первое, что нужно сделать в подобных ситуациях — постараться объяснить увиденное. Быть может, доказательство поможет нам найти такое объяснение, а может быть, и нет. Рассмотрим векторный и алгебраический подход к этой теореме. Нужно доказать, что точки А, В, С и D , которые являются серединами сторон произвольного четырехугольника PQRS , определяют параллелограмм. Иными словами, нужно доказать, что векторы АВ → и DC → равны, то есть их можно разложить на одинаковые составляющие. Пусть исходные точки имеют следующие координаты: P( p 1, р 2 ), Q( q 1, q 2 ), R( r 1, r 2 ) и S( s 1, s 2 ). Найдем координаты первого из рассматриваемых векторов и покажем, что они равны координатам второго вектора:
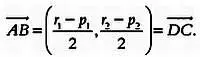
Теорема доказана. Объясняет ли это доказательство суть увиденного нами? Нет. Перед нами пример того, как логика доказывает, но не объясняет. В данном случае логика не объясняет, потому что из доказательства мы не можем понять, почему ситуация складывается именно так, а не иначе. Вернемся в начало доказательства и обратим внимание на часть исходной фигуры:

Возможно, в этом контексте она покажется вам знакомой. Проведем вспомогательную линию — единственно возможную для завершения рисунка:

Результат построения — треугольники APD и QPS . Так как точки А и D — середины сторон PQ и PS соответственно, то отрезок AD параллелен QS , а его длина в два раза меньше длины QS . Последнее утверждение известно как теорема о средней линии — она заслуживает отдельного упоминания, так как не столь очевидна, как может показаться.
Читать дальше


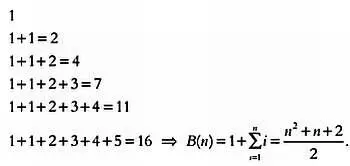

 кривая — гипербола, которая описывается уравнением:
кривая — гипербола, которая описывается уравнением: