Микель Альберти - Мир математики. т.20. Творчество в математике. По каким правилам ведутся игры разума

только числа, которые являются степенями 2, нельзя представить как сумму последовательных натуральных чисел.

Приведя подобные слагаемые в суммах последовательных чисел, увидим, откуда появляется этот нечетный множитель:

Если число слагаемых n нечетное, этим нечетным множителем будет n , если же число слагаемых n четное, то этим нечетным множителем будет 2 n + 1. В любом случае один из сомножителей будет нечетным.

* * *

КАРЛ ФРИДРИХ ГАУСС(1777–1855)

Этот немецкий математик, который родился в Брауншвейге и умер в Гёттингене, был вундеркиндом. Он получил хорошее образование благодаря не отцу, а матери. Гаусс никак не мог решить, что ему следует изучать — философию или математику. В начале весны 1796 года он сделал выбор в пользу математики, и наука весьма благодарна ему за это, так как Гаусс в итоге стал одним из величайших математиков всех времен. Несомненно, на его решение повлиял тот факт, что в тот самый весенний день ему удалось построить с помощью циркуля и линейки правильный 17-угольник. Как математик Гаусс совершил много важных открытий, но этим успехом он гордился больше всего — настолько, что попросил высечь этот многоугольник на своем надгробии, на что мастер возразил, что высечь эту фигуру будет очень сложно и ее будет почти невозможно отличить от окружности.

Портрет Гаусса .

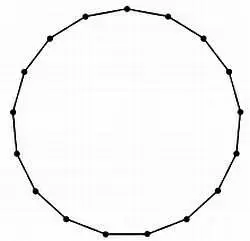
Этот немецкий математик доказал, что правильный 17-угольник можно построить с помощью циркуля и линейки.

До сих пор мы говорили о наиболее типичном аспекте математической деятельности — о том, как человек, сталкивающийся с событиями и явлениями, пытается объяснить их с точки зрения математики. Мы не углублялись в культурные и социальные аспекты математики, хотя в первой главе отметили, что именно они играют основную роль в ее развитии.

Математика формируется в рамках определенного социального и культурного контекста, который в значительной степени определяет ее развитие как внутри научной среды, так и вне ее. Следовательно, социокультурные факторы влияют на математическое творчество, так как придают одним задачам большую важность, чем другим, и если в одной культуре определенные задачи считаются очень важными, то в другой культурной среде им не уделяется никакого внимания.

Этноматематика — это раздел науки, изучающий развитие математики в определенных группах культур. Благодаря этноматематике мы знаем, что в разных частях света люди по-разному производят вычисления, по-своему воспринимают геометрические фигуры и используют для решения одних и тех же задач разные алгоритмы. С одной стороны, это доказывает творческую природу каждой культуры, с другой стороны — делает возможным межкультурное взаимодействие.

Далее мы вкратце расскажем о том, как автор этой книги накапливал новые математические знания вне своей научной среды и вне родной ему западной культуры. Надеемся, что читатель снисходительно отнесется к крайне субъективному характеру повествования.

Пока что мы всегда говорили об эвристике в рамках определенной культуры — как в пределах академической среды, так и за ними. Теперь мы выйдем за рамки нашей культурной парадигмы и посмотрим, как математическое творчество соотносится с различными культурными и социальными аспектами, как оно связано с ними.

Мы уже говорили, что первый шаг на пути к математическому творчеству — это начать задавать вопросы о том, что нас окружает. Что может быть лучше, чем выйти из дома и начать наблюдать, изучать новое, испытывать незнакомые ощущения?

Математики нечасто путешествуют. Мы не имеем в виду путешествия, связанные с научной работой, которые проходят в привычном для ученых контексте. Мы говорим о путешествиях с целью узнать что-то новое, познакомиться с новыми людьми, новыми культурами и обычаями, новым образом жизни и образом мыслей. К таким путешествиям не относятся организованные поездки, так как в них туриста окружает значительная часть привычной среды — хотя бы минимальные удобства, транспорт, гид-переводчик и попутчики, принадлежащие к родной культуре.