Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

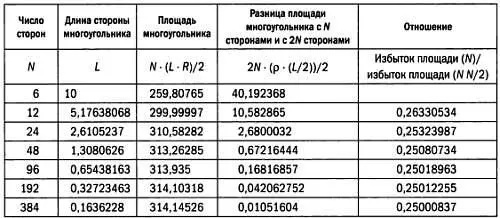
В 480 году этот метод был пересмотрен математиком и астрономом Цзу Чунчжи(429–500) , жившим во времена династии Ци. Использовав многоугольник с 12288 = 3·2 12сторонами, он определил, что π заключено между следующими значениями: 3,1415926 < π < 3,1415927. Он представил результат так:

π ~= 355/113. В течение 900 лет эта оценка оставалась наиболее точной.

История науки гласит, что индийская математика возникла в VII веке, когда в этой стране в качестве всеобщего языка уже использовался санскрит. Индия не была изолированной от Европы: индийцы поддерживали тесные контакты с греками, позднее с римлянами. Не следует забывать, что граница империи Александра Македонского проходила по долине реки Инд.

Хотя индийские ученые уделяли особое внимание астрономии, они занимались и математикой, которая играла важнейшую роль в развитии научной мысли. Любопытно, что индийцы не разделяли подход к науке, принятый в странах Востока, и не считали, что она обязательно должна иметь практическое применение. Стимулом развития индийской математики было получение знаний ради самих знаний. Несмотря на это, индийские ученые не слишком охотно приводили более или менее формальные доказательства своих методов и алгоритмов. Считается, что они обосновывали свои открытия, но найденные ими доказательства не сохранились.

Индийцы подробно изучили тригонометрию, особенно применительно к астрономическим расчетам и решениям неопределенных уравнений, а также алгебру и комбинаторику. По сути, понятие синуса и само слово «синус» впервые упоминаются в трактате по астрономии V века «Пайтамаха-сиддханта».

* * *

СИНУС

Как случилось, что для обозначения тригонометрической функции стало использоваться слово «синус»? Эта история берет начало в индийском трактате по астрономии под названием «Пайтамаха-сиддханта», в котором приводится таблица джайя-ардха — «измерение струн», использовавшаяся в астрономических расчетах. Этот термин вновь упоминается в труде «Ариабхатия» индийского математика Ариабхаты, который обозначал его как «джайя», или «джива». Арабы перевели это слово как «джиба», но так как в арабском отсутствуют отдельные буквы для обозначения гласных, то это слово записывалось как джб. При более позднем прочтении случайно или умышленно джб было прочитано как джаиб, что означало «грудь» или «пазуха», а переводчики на латынь использовали слово «синус», означавшее «пазуха», «складка на тоге», а также «залив». Этот термин используется не только в романских языках: даже английское слово sine имеет латинское происхождение.

* * *

Нет сомнений, что важнейшим вкладом индийских математиков в науку была созданная ими система счисления, которую мы называем арабской. В действительности арабы заимствовали ее у индийцев. Индийские цифры произошли от системы записи, которая использовалась во времена короля Ашоки(272–231 гг. до н. э.) для записи текстов на древнем языке пракрите. Тем не менее по пути на Запад индийские цифры неоднократно видоизменялись, поэтому современные цифры не похожи на придуманные индийцами. Современные цифры — одна из версий древних цифр на пракрите, которые попали в Северную Африку, претерпев некоторые изменения, и стали известны в Европе в Средние века.

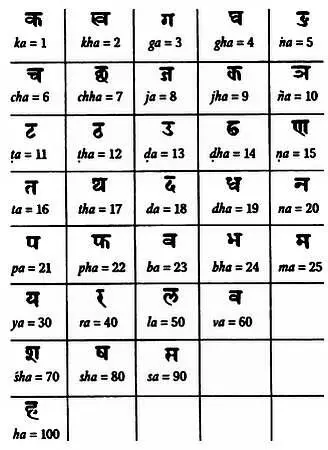
Некоторые индийские цифры, описанные математиком Ариабхатой.

(Источник: Джордж Ифра, «Всеобщая история чисел».)

Позиционная система счисления также имеет индийское происхождение. Изначально индийцы записывали числа с помощью символов, обозначавших цифры от 1 до 9; десятки от 10 до 90 обозначались другими цифрами. Числа, кратные 100, 1000 и так далее обозначались символами, соответствовавшими единицам, рядом с которыми записывались символы, обозначавшие 100, 1000 и далее. Позднее эта система записи упростилась, и впервые в истории возникла позиционная система счисления, в которой использовались только символы, соответствующие цифрам от 0 до 9. Когда именно произошло это изменение, точно неизвестно, но большинство источников указывает в качестве наиболее вероятной даты 600 год. Так, в сирийском тексте 662 года уже используются индийские цифры.